摘要:CD ⊥BF BF⊥平面CDB1 EF为BE在平面CDB1内的射影
网址:http://m.1010jiajiao.com/timu_id_501920[举报]
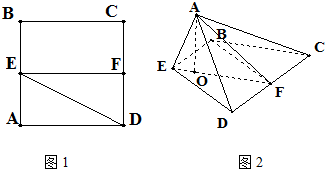 已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.
已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.(1)证明:BF∥平面ADE;
(2)证明:AE⊥平面ACD;
(3)求三棱锥F-ABC的体积.
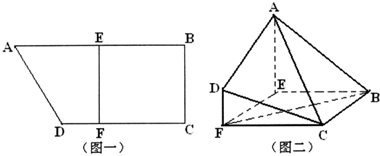 (2011•徐州模拟)在直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,过E作EF⊥CD,垂足为F,(如图一),将此梯形沿EF折起,使得平面ADFE垂直于平面FCBE,(如图二).
(2011•徐州模拟)在直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,过E作EF⊥CD,垂足为F,(如图一),将此梯形沿EF折起,使得平面ADFE垂直于平面FCBE,(如图二).(1)求证:BF∥平面ACD;
(2)求多面体ADFCBE的体积.
(2011•松江区二模)已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,沿EF将梯形ABCD翻折,使AE⊥平面EBCF(如图).设AE=x,四面体DFBC的体积记为f(x).
(1)写出f(x)表达式,并求f(x)的最大值;
(2)当x=2时,求二面角D-BF-E的余弦值.

查看习题详情和答案>>
| π | 2 |
(1)写出f(x)表达式,并求f(x)的最大值;
(2)当x=2时,求二面角D-BF-E的余弦值.


 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=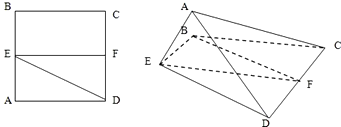 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).