题目内容
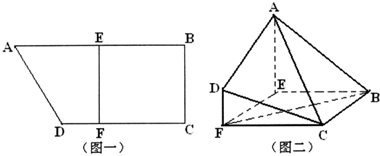 (2011•徐州模拟)在直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,过E作EF⊥CD,垂足为F,(如图一),将此梯形沿EF折起,使得平面ADFE垂直于平面FCBE,(如图二).
(2011•徐州模拟)在直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,过E作EF⊥CD,垂足为F,(如图一),将此梯形沿EF折起,使得平面ADFE垂直于平面FCBE,(如图二).(1)求证:BF∥平面ACD;
(2)求多面体ADFCBE的体积.
分析:(1)先证明BCFE为正方形,AE和DF都垂直于平面BCFE,设O是正方形BCFE的中心,取AC得中点为H,证明四边形OHDF为矩形,OF平行于DH,再由直线和平面平行的判定定理可得OF∥平面ACD,即BF∥平面ACD.
(2)把多面体ADFCBE分成两个棱锥:三棱锥A-BCE 和四棱锥C-AEFD,分别求出 VA-BCE和 VC-AEFD 的值,相加即得所求.
(2)把多面体ADFCBE分成两个棱锥:三棱锥A-BCE 和四棱锥C-AEFD,分别求出 VA-BCE和 VC-AEFD 的值,相加即得所求.
解答:解:(1)证明:∵直角梯形ABCD中,AB∥CD,AB=2BC=4,CD=3,E为AB中点,EF⊥CD,垂足为F,∴BCFE为正方形.
设BF和CE的交点为O,则O是正方形BCFE的中心.
再由平面ADFE垂直于平面FEBC,可得AE和DF都垂直于平面BCFE.
取AC得中点为H,则由三角形的中位线性质可得OH平行且等于AE的一半,故OH平行且等于DF,故四边形OHDF为矩形,故OF平行于DH.
再由DH?平面ACD,OF不在平面ACD内,故OF∥平面ACD,即BF∥平面ACD.
 (2)把多面体ADFCBE分成两个棱锥:三棱锥A-BCE 和四棱锥C-AEFD,
(2)把多面体ADFCBE分成两个棱锥:三棱锥A-BCE 和四棱锥C-AEFD,
由题意可得CF⊥平面AEFD,AE⊥平面BCFE.
∴VA-BCE=
S△BCE•AE=
×
×BC•BE•AE=
=
.
VC-AEFD=
×SAEFD•CF=
×
(AE+DF)•EF•CF=
×(2+1)×2×2=2,
故多面体ADFCBE的体积为 VA-BCE+VC-AEFD=
+2=
.
设BF和CE的交点为O,则O是正方形BCFE的中心.
再由平面ADFE垂直于平面FEBC,可得AE和DF都垂直于平面BCFE.
取AC得中点为H,则由三角形的中位线性质可得OH平行且等于AE的一半,故OH平行且等于DF,故四边形OHDF为矩形,故OF平行于DH.
再由DH?平面ACD,OF不在平面ACD内,故OF∥平面ACD,即BF∥平面ACD.
 (2)把多面体ADFCBE分成两个棱锥:三棱锥A-BCE 和四棱锥C-AEFD,
(2)把多面体ADFCBE分成两个棱锥:三棱锥A-BCE 和四棱锥C-AEFD,由题意可得CF⊥平面AEFD,AE⊥平面BCFE.
∴VA-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 23 |
| 6 |
| 4 |
| 3 |
VC-AEFD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故多面体ADFCBE的体积为 VA-BCE+VC-AEFD=
| 4 |
| 3 |
| 10 |
| 3 |
点评:本题主要考查直线和平面平行的判定定理的应用,用“分割法”求棱锥的体积,属于中档题.

练习册系列答案
相关题目
 (2011•徐州模拟)在平面直角坐标系xOy中,已知圆B:(x-1)2+y2=16与点A(-1,0),P为圆B上的动点,线段PA的垂直平分线交直线PB于点R,点R的轨迹记为曲线C.
(2011•徐州模拟)在平面直角坐标系xOy中,已知圆B:(x-1)2+y2=16与点A(-1,0),P为圆B上的动点,线段PA的垂直平分线交直线PB于点R,点R的轨迹记为曲线C.