摘要:(Ⅱ)当时.点的坐标是. 取.
网址:http://m.1010jiajiao.com/timu_id_501454[举报]
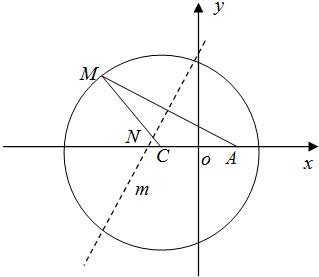 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.(1)证明曲线E是椭圆,并写出当a=2时该椭圆的标准方程;
(2)设直线l过点C和椭圆E的上顶点B,点A关于直线l的对称点为点Q,若椭圆E的离心率e∈[
| 1 |
| 2 |
| ||
| 2 |
设点A,B的坐标分别为(-a,0),(a,0).直线AM,BM相交于点M,且他们的斜率之积为k.则下列说法正确的是
(1)当k=
时,点M的轨迹是双曲线.(其中a,b∈R+)
(2)当k=-
时,点M的轨迹是部分椭圆.(其中a,b∈R+)
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
,0),F2(
,0),且|PF1|=
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
]
(4)在(2)的条件下,过点F1(-
,0),F2(
,0).满足
•
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是(
,1).
查看习题详情和答案>>
(2)(3)
(2)(3)
(1)当k=
| b2 |
| a2 |
(2)当k=-
| b2 |
| a2 |
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
| a2+b2 |
| a2+b2 |
| 1 |
| 4 |
| 5 |
| 3 |
(4)在(2)的条件下,过点F1(-
| a2-b2 |
| a2-b2 |
. |
| MF1 |
. |
| MF2 |
| ||
| 2 |
设点A,B的坐标分别为(-a,0),(a,0).直线AM,BM相交于点M,且他们的斜率之积为k.则下列说法正确的是________
(1)当k= 时,点M的轨迹是双曲线.(其中a,b∈R+)
时,点M的轨迹是双曲线.(其中a,b∈R+)
(2)当k=- 时,点M的轨迹是部分椭圆.(其中a,b∈R+)
时,点M的轨迹是部分椭圆.(其中a,b∈R+)
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-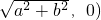 ,F2(
,F2( ,0),且|PF1|=
,0),且|PF1|= |PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1, ]
]
(4)在(2)的条件下,过点F1(- ,0),F2(
,0),F2( ,0).满足
,0).满足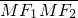 =0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是 .
.
查看习题详情和答案>>
设点A,B的坐标分别为(-a,0),(a,0).直线AM,BM相交于点M,且他们的斜率之积为k.则下列说法正确的是______
(1)当k=
时,点M的轨迹是双曲线.(其中a,b∈R+)
(2)当k=-
时,点M的轨迹是部分椭圆.(其中a,b∈R+)
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
,0),F2(
,0),且|PF1|=
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
]
(4)在(2)的条件下,过点F1(-
,0),F2(
,0).满足
•
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是(
,1).
查看习题详情和答案>>
(1)当k=
| b2 |
| a2 |
(2)当k=-
| b2 |
| a2 |
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
| a2+b2 |
| a2+b2 |
| 1 |
| 4 |
| 5 |
| 3 |
(4)在(2)的条件下,过点F1(-
| a2-b2 |
| a2-b2 |
| . |
| MF1 |
| . |
| MF2 |
| ||
| 2 |
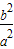 时,点M的轨迹是双曲线.(其中a,b∈R+)
时,点M的轨迹是双曲线.(其中a,b∈R+)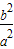 时,点M的轨迹是部分椭圆.(其中a,b∈R+)
时,点M的轨迹是部分椭圆.(其中a,b∈R+)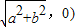 ,F2(
,F2(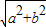 ,0),且|PF1|=
,0),且|PF1|= |PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1, ]
]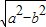 ,0),F2(
,0),F2(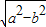 ,0).满足
,0).满足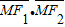 =0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是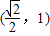 .
.