题目内容
设点A,B的坐标分别为(-a,0),(a,0).直线AM,BM相交于点M,且他们的斜率之积为k.则下列说法正确的是
(1)当k=
时,点M的轨迹是双曲线.(其中a,b∈R+)
(2)当k=-
时,点M的轨迹是部分椭圆.(其中a,b∈R+)
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
,0),F2(
,0),且|PF1|=
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
]
(4)在(2)的条件下,过点F1(-
,0),F2(
,0).满足
•
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是(
,1).
(2)(3)
(2)(3)
(1)当k=
| b2 |
| a2 |
(2)当k=-
| b2 |
| a2 |
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
| a2+b2 |
| a2+b2 |
| 1 |
| 4 |
| 5 |
| 3 |
(4)在(2)的条件下,过点F1(-
| a2-b2 |
| a2-b2 |
. |
| MF1 |
. |
| MF2 |
| ||
| 2 |
分析:设出动点M的坐标,写出直线AM,BM的斜率,由斜率之积等于k求出轨迹方程,若k=
时,得到M的轨迹是除去两个顶点的双曲线;若k=-
时,得到M的轨迹是椭圆除去长轴上两个顶点;是双曲线时,由题目给出的|PF1|=
|PF2|,集合双曲线定义求出|PF1|和|PF2|的长度,由两边之和大于第三边列式求离心率范围;是椭圆时,根据与两焦点连线互相垂直的点总在椭圆内部,取椭圆短轴上的一个端点,由该点到两个焦点距离的平方和大于焦距的平方求得椭圆的离心率小于
,按以上分析可以判断出正确命题的个数.
| b2 |
| a2 |
| b2 |
| a2 |
| 1 |
| 4 |
| ||
| 2 |
解答:解:设M(x,y),由A,B的坐标分别为(-a,0),(a,0),
则kAM=
(x≠-a),kBM=
(x≠a),
由kAM•kBM=k,得:
•
=k,即kx2-y2=ka2①.
(1)若k=
(a,b∈R+),则方程①化为
-
=1,点M的轨迹是双曲线除去两个顶点,
∴命题(1)不正确;
(2)若k=-
(a,b∈R+),则方程①化为
+
=1,点M的轨迹是椭圆除去长轴上两个顶点,
∴命题(2)正确;
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点,说明点P在双曲线
-
=1的左支上,
F1,F2是双曲线的左右焦点,则由|PF1|=
|PF2|及|PF2|-|PF1|=2a求得|PF1|=
a,|PF2|=
a,
又|PF1|+|PF2|=
a+
a≥2c,∴
≤
,又e>1,∴(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
].
∴命题(3)正确;
(4)在(2)的条件下,由满足
•
=0的点M总在曲线的内部,说明满足MF1⊥MF2的点M在曲线内部,若点M在曲线上,则|MF1|2+|MF2|2>4c2,取M为椭圆短轴的一个端点,则|MF1|=|MF2|=a,所以2a2>4c2,
则
<
.∴命题(4)错误.
所以,正确的命题是②③.
故答案为②③.
则kAM=
| y |
| x+a |
| y |
| x-a |
由kAM•kBM=k,得:
| y |
| x+a |
| y |
| x-a |
(1)若k=
| b2 |
| a2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴命题(1)不正确;
(2)若k=-
| b2 |
| a2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴命题(2)正确;
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点,说明点P在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
F1,F2是双曲线的左右焦点,则由|PF1|=
| 1 |
| 4 |
| 2 |
| 3 |
| 8 |
| 3 |
又|PF1|+|PF2|=
| 2 |
| 3 |
| 8 |
| 3 |
| c |
| a |
| 5 |
| 3 |
| 5 |
| 3 |
∴命题(3)正确;
(4)在(2)的条件下,由满足
. |
| MF1 |
. |
| MF2 |
则
| c |
| a |
| ||
| 2 |
所以,正确的命题是②③.
故答案为②③.
点评:本题考查了命题的真假判断及简单应用,考查了椭圆和双曲线的简单几何性质,涉及求圆锥曲线的离心率范围问题,关键是根据题目给出的条件得到关于a和c的不等式,此题是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
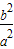 时,点M的轨迹是双曲线.(其中a,b∈R+)
时,点M的轨迹是双曲线.(其中a,b∈R+)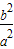 时,点M的轨迹是部分椭圆.(其中a,b∈R+)
时,点M的轨迹是部分椭圆.(其中a,b∈R+)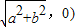 ,F2(
,F2(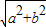 ,0),且|PF1|=
,0),且|PF1|= |PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1, ]
]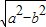 ,0),F2(
,0),F2(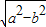 ,0).满足
,0).满足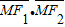 =0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是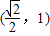 .
.