摘要:设平面的法向量为...所以
网址:http://m.1010jiajiao.com/timu_id_497773[举报]
请先阅读:
设平面向量![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),且
=(b1,b2),且![]() 与
与![]() 的夹角为è,
的夹角为è,
因为![]() •
•![]() =|
=|![]() ||
||![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() ||
||![]() |.
|.
即![]() ,
,
当且仅当è=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有![]() 成立;
成立;
(II)试求函数![]() 的最大值.
的最大值.
请先阅读:
设平面向量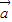 =(a1,a2),
=(a1,a2),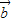 =(b1,b2),且
=(b1,b2),且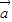 与
与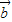 的夹角为θ,
的夹角为θ,
因为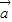 •
•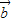 =|
=|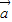 ||
||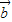 |cosθ,
|cosθ,
所以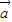 •
•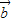 ≤|
≤|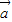 ||
||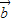 |.
|.
即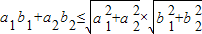 ,
,
当且仅当θ=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有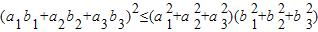 成立;
成立;
(II)试求函数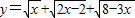 的最大值.
的最大值.
查看习题详情和答案>>
设平面向量
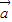 =(a1,a2),
=(a1,a2),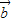 =(b1,b2),且
=(b1,b2),且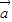 与
与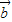 的夹角为θ,
的夹角为θ,因为
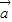 •
•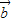 =|
=|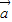 ||
||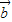 |cosθ,
|cosθ,所以
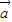 •
•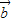 ≤|
≤|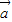 ||
||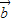 |.
|.即
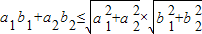 ,
,当且仅当θ=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有
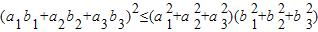 成立;
成立;(II)试求函数
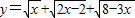 的最大值.
的最大值.查看习题详情和答案>>
如图,四棱柱 中,
中,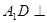 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 .
.

(1)求三棱锥 的体积;
的体积;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一点
上存在一点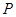 ,使得
,使得 ,当二面角
,当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
【解析】(1)在 中,
中,
 .
(3’)
.
(3’)
(2)以点D为坐标原点,建立如图所示的空间直角坐标系 ,则
,则
 (4’)
(4’)
 ,设平面
,设平面 的法向量为
的法向量为 ,
,
由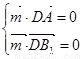 得
得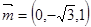 ,
(5’)
,
(5’)
则 ,
,
 . (7’)
. (7’)
(3)
设平面 的法向量为
的法向量为 ,由
,由 得
得 ,
(10’)
,
(10’)

查看习题详情和答案>>
 DE∥BC∴
DE∥BC∴ ∴
∴ ∴
∴ ∴
∴ 又∵
又∵ ∴
∴



 的法向量为
的法向量为 ,则
,则 ,又
,又 ,
, ,所以
,所以 ,令
,令 ,则
,则 ,所以
,所以 ,
, 。因为
。因为 ,
,
 。
。