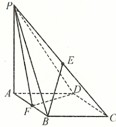
摘要:16.在四棱锥P-ABCD中.∠ABC=∠ACD=90°.∠BAC=∠CAD=60°.PA⊥平面ABCD.E为PD的中点.PA=2AB=2.(Ⅰ)求四棱锥P-ABCD的体积V,(Ⅱ)若F为PC的中点.求证PC⊥平面AEF,
网址:http://m.1010jiajiao.com/timu_id_497670[举报]
 (本小题满分14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD与底面ABCD垂直,PD=DC,E是PC的中点,作EF
(本小题满分14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD与底面ABCD垂直,PD=DC,E是PC的中点,作EF![]() 于点F(Ⅰ)证明PA
于点F(Ⅰ)证明PA![]() 平面EBD.
平面EBD.
(Ⅱ)证明PB![]() 平面EFD.
平面EFD.
(Ⅲ)求二面角![]() 的余弦值;
的余弦值;
(本小题满分14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,
∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(1)求证:PC⊥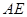 ;
;
(2)求证:CE∥平面PAB;
(3)求三棱锥P-ACE的体积V.
查看习题详情和答案>>
(本小题满分14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(1)求证:PC⊥![]() ;
;
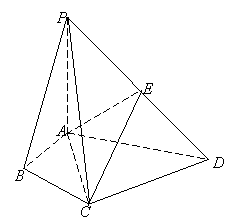 (2)求证:CE∥平面PAB;
(2)求证:CE∥平面PAB;
(3)求三棱锥P-ACE的体积V.
查看习题详情和答案>>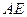 ;
;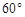 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.