摘要:△AQF的外接圆圆心为(a.0).半径r=|FQ|=a
网址:http://m.1010jiajiao.com/timu_id_497331[举报]
1.(1)因为.files/image386.gif) ,所以
,所以.files/image388.gif)
又.files/image134.gif) 是圆O的直径,所以
是圆O的直径,所以.files/image391.gif)
又因为.files/image393.gif) (弦切角等于同弧所对圆周角)
(弦切角等于同弧所对圆周角)
所以.files/image395.gif) 所以
所以.files/image397.gif)
又因为.files/image399.gif) ,所以
,所以.files/image401.gif) 相似
相似
所以.files/image403.gif) ,即
,即.files/image158.gif)
(2)因为.files/image153.gif) ,所以
,所以.files/image406.gif) ,
,
因为.files/image151.gif) ,所以
,所以.files/image409.gif)
由(1)知:.files/image411.gif) 。所以
。所以.files/image413.gif)
所以.files/image415.gif) ,即圆的直径
,即圆的直径.files/image417.gif)
又因为.files/image419.gif) ,即
,即.files/image421.gif)
解得.files/image423.gif)
2.依题设有:.files/image425.gif)
令.files/image427.gif) ,则
,则.files/image429.gif)
.files/image431.gif)
.files/image429.gif)
.files/image433.gif)
.files/image435.gif)
.files/image435.gif)
.files/image438.gif)
3.将极坐标系内的问题转化为直角坐标系内的问题
点.files/image440.gif) 的直角坐标分别为
的直角坐标分别为.files/image442.gif)
故.files/image444.gif) 是以
是以.files/image140.gif) 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,
进而易知圆心为.files/image447.gif) ,半径为
,半径为.files/image449.gif) ,圆的直角坐标方程为
,圆的直角坐标方程为
.files/image451.gif) ,即
,即.files/image453.gif)
将.files/image455.gif) 代入上述方程,得
代入上述方程,得
.files/image457.gif) ,即
,即.files/image459.gif)
4.假设.files/image461.gif) ,因为
,因为.files/image463.gif) ,所以
,所以.files/image465.gif) 。
。
又由.files/image467.gif) ,则
,则.files/image469.gif) ,
,
所以.files/image471.gif) ,这与题设矛盾
,这与题设矛盾
又若.files/image473.gif) ,这与
,这与.files/image463.gif) 矛盾
矛盾
综上可知,必有.files/image475.gif) 成立
成立
同理可证.files/image477.gif) 也成立
也成立
命题成立
5. 解:由a1=S1,k=.files/image479.gif) .下面用数学归纳法进行证明.
.下面用数学归纳法进行证明.
1°.当n=1时,命题显然成立;
2°.假设当n=k(k.files/image481.gif) N*)时,命题成立,
N*)时,命题成立,
即1?2?3+2?3?4+……+ k(k+1)(k+2)=.files/image479.gif) k(k+1)(k+2)(k+3),
k(k+1)(k+2)(k+3),
则n=k+1时,1?2?3+2?3?4+……+ k(k+1)(k+2)+(k+1)(k+2)(k+3)=.files/image479.gif) k(k+1)(k+2)(k+3)+(k+1)(k+2)(k+3)
k(k+1)(k+2)(k+3)+(k+1)(k+2)(k+3)
=.files/image479.gif) ( k+1)(k+1+1)(k+1+2)(k+1+3)
( k+1)(k+1+1)(k+1+2)(k+1+3)
即命题对n=k+1.成立
由1°, 2°,命题对任意的正整数n成立.
6.(1)因为.files/image483.gif) ,
,.files/image485.gif) ,
,
.files/image487.gif) ,所以
,所以.files/image489.gif)
故事件A与B不独立。
(2)因为.files/image491.gif)
.files/image493.gif)
所以.files/image495.gif)
.files/image496.gif)
(2012•孝感模拟)已知集合M={1,2,3},N={1,2,3,4},定义函数f:M→N.若点A(1,f(1)),B(2,f(2)),C(3,f(3)),△ABC的外接圆圆心为D,且
+
=γ
(γ∈R),则满足条件的函数f(x)有( )
| DA |
| DC |
| DB |
查看习题详情和答案>>
 如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(-4,0)D(0,4)设△AOB的外接圆圆心为E.
如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(-4,0)D(0,4)设△AOB的外接圆圆心为E.(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
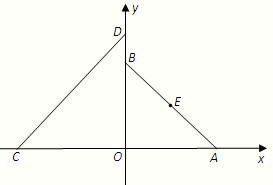 如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(-4,0),D(0,4),设△AOB的外接圆圆心为E.
如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(-4,0),D(0,4),设△AOB的外接圆圆心为E.