摘要:当时.得. -----12分
网址:http://m.1010jiajiao.com/timu_id_49466[举报]
(12分)甲、乙二人各有6张扑克牌,每人都是3张红心,2张草花,1张方片。每次两人从自己的6张牌中任意抽取一张进行比较,规定:两人花色相同时甲胜,花色不同时乙胜。
(Ⅰ)此规定是否公平?为什么?
(Ⅱ)若又规定:当甲取红心、草花、方片而获胜所得的分数分别为3、2、1,否则得0分,求甲得分的期望.
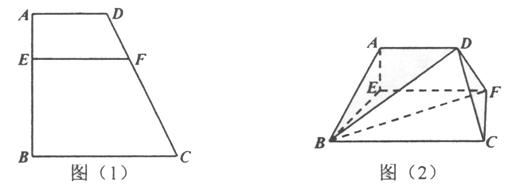
查看习题详情和答案>>(12分)已知如图(1),梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,设
,设![]() (
(![]() )。沿
)。沿![]() 将梯形
将梯形![]() 翻折,使平面
翻折,使平面![]() 平面
平面![]() ,如图(2)。
,如图(2)。
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)当![]() 取得最大值时,求二面角
取得最大值时,求二面角![]() 的正弦值.
的正弦值.
(12分)设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,![]() )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线![]() 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
围.
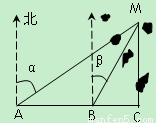
查看习题详情和答案>> 处测得某岛
处测得某岛 的方位角为北偏东
的方位角为北偏东 角,前进
角,前进
 后在
后在 处测得该岛的方位角为北偏东
处测得该岛的方位角为北偏东 角,已知该岛周围
角,已知该岛周围
 ,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自
,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自
 处测得某岛
处测得某岛 的方位角为北偏东
的方位角为北偏东 角,前进
角,前进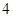
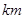 后在
后在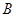 处测得该岛的方位角为北偏东
处测得该岛的方位角为北偏东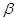 角,已知该岛周围
角,已知该岛周围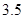
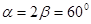 ,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自
,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自