摘要:(Ⅱ)设平面AMN与PAB所成锐二面角的大小为,作,则故所求平面AMN与PAB所成锐二面角的大小为----
网址:http://m.1010jiajiao.com/timu_id_49449[举报]
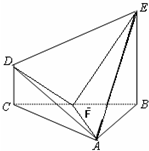
 (2010•福建模拟)如图,l1、l2是两条互相垂直的异面直线,点P、C在直线l1上,点A、B在直线l2上,M、N分别是线段AB、AP的中点,且PC=AC=a,PA=
(2010•福建模拟)如图,l1、l2是两条互相垂直的异面直线,点P、C在直线l1上,点A、B在直线l2上,M、N分别是线段AB、AP的中点,且PC=AC=a,PA=| 2 |
(Ⅰ)证明:PC⊥平面ABC;
(Ⅱ)设平面MNC与平面PBC所成的角为θ(0°<θ≤90°).现给出下列四个条件:
①CM=
| 1 |
| 2 |
| 2 |
请你从中再选择两个条件以确定cosθ的值,并求之.
 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=| π | 2 |
(1)设平面ABE与平面ACD的交线为直线l,求证:l∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积.
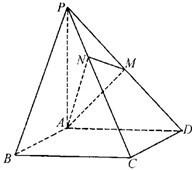 如图,已知四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在侧棱PD、PC上,且PM=MD.
如图,已知四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在侧棱PD、PC上,且PM=MD.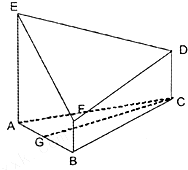 已知△ABC是正三角形,GC是△ABC的中线,EA、FB、CD都垂直于平面ABC.EA=3a,AB=CD=2a,FB=a,设平面EDF与平面ABC的交线为l.
已知△ABC是正三角形,GC是△ABC的中线,EA、FB、CD都垂直于平面ABC.EA=3a,AB=CD=2a,FB=a,设平面EDF与平面ABC的交线为l.