题目内容

（2010•福建模拟）如图，l1、l2是两条互相垂直的异面直线，点P、C在直线l1上，点A、B在直线l2上，M、N分别是线段AB、AP的中点，且PC=AC=a，PA=
2
a．
（Ⅰ）证明：PC⊥平面ABC；
（Ⅱ）设平面MNC与平面PBC所成的角为θ（0°＜θ≤90°）．现给出下列四个条件：
①CM=
1
2
AB；②AB=
2
a；③CM⊥AB；④BC⊥AC．
请你从中再选择两个条件以确定cosθ的值，并求之．
分析：（I）在△PAC中根据PC=AC=a，PA=
2
a，三边满足勾股定理则PC⊥AC，根据题意可知PC⊥AB，又AC∩AB=A，满足线面垂直的判定定理，从而得证；
（II）本小问具有开放性，选择②④可确定cosθ的大小，根据AC⊥BC，且AB=
2
a，AC=a则BC=a，以C为坐标原点，
CB
、
CA
、
CP
的方向为x、y、z轴正方向建立空间直角坐标系，
CA
=（0，a，0）是平面PBC的一个法向量，然后求出平面MNC的法向量
n
，然后根据cos＜
n
，
CA
＞=
n
•
CA
|n|
• 
|CA|
，从而求出cosθ的值．
解答：证明：（I）在△PAC中∵PC=AC=a，PA=
2
a．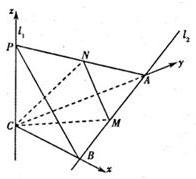
∴PC2+AC2=PA2，∴PC⊥AC
∵l1、l2是两条互相垂直的异面直线，点P、C在直线l1上，点A、B在直线l2上，
∴PC⊥AB，又AC∩AB=A
∴PC⊥平面ABC
（II）选择②④可确定cosθ的大小
∵AC⊥BC，且AB=
2
a，AC=a
∴BC=a
以C为坐标原点，
CB
、
CA
、
CP
的方向为x、y、z轴正方向建立空间直角坐标系
则C（0，0，0），B（a，0，0），A（0，a，0），P（0，0a）
又M、N分别是线段AB、AP的中点，
∴M（
a
2
，
a
2
，0），N（0，
a
2
，
a
2
）
∵CA⊥平面PBC
∴
CA
=（0，a，0）是平面PBC的一个法向量
设平面MNC的法向量
n
=（x，y，z）
由
n
⊥
CN
n
⊥
CM
得
a
2
y+
a
2
z=0
a
2
x+
a
2
y=0

取x=1，得
n
=（1，-1，1）为平面MNC的一个法向量
∴cos＜
n
，
CA
＞=
n
•
CA
|n|
• 
|CA|
=
-a
3
a
=-
3
3

∴cosθ=
3
3
点评：本题主要考查了直线与平面垂直的判定，以及用空间向量求平面间的夹角，同时考查了开放性问题，属于中档题．
练习册系列答案
相关题目
（2010•福建模拟）考察等式：
C
0
m
C
r
n-m
+
C
1
m
C
r-1
n-m
+…+
C
r
m
C
0
n-m
=
C
r
n
（*），其中n、m、r∈N*，r≤m＜n且r≤n-m．某同学用概率论方法证明等式（*）如下：
设一批产品共有n件，其中m件是次品，其余为正品．现从中随机取出r件产品，
记事件Ak={取到的r件产品中恰有k件次品}，则P(Ak)=
C
k
m
C
r-k
n-m
C
r
n
，k=0，1，2，…，r．
显然A0，A1，…，Ar为互斥事件，且A0∪A1∪…∪Ar=Ω（必然事件），
因此1=P（Ω）=P（A0）+P（A1）+…P（Ar）=
C
0
m
C
r
n-m
+
C
1
m
C
r-1
n-m
+…+
C
r
m
C
0
n-m
C
r
n
，
所以
C
0
m
C
r
n-m
+
C
1
m
C
r-1
n-m
+…+
C
r
m
C
0
n-m
=
C
r
n
，即等式（*）成立．
对此，有的同学认为上述证明是正确的，体现了偶然性与必然性的统一；但有的同学对上述证明方法的科学性与严谨性提出质疑．现有以下四个判断：
①等式（*）成立  ②等式（*）不成立  ③证明正确  ④证明不正确
试写出所有正确判断的序号
①③
①③
．
（2010•福建模拟）已知函数f（x）=（ax2+bx+c）ex在x=1处取得极小值，其图象过点A（0，1），且在点处切线的斜率为-1．
（Ⅰ）求f（x）的解析式；
（Ⅱ）设函数g（x）的定义域D，若存在区间[m，n]⊆D，使得g（x）在[m，n]上的值域也是[m，n]，则称区间[m，n]为函数g（x）的“保值区间”．
（ⅰ）证明：当x＞1时，函数f（x）不存在“保值区间”；
（ⅱ）函数f（x）是否存在“保值区间”？若存在，写出一个“保值区间”（不必证明）；若不存在，说明理由．
（2010•福建模拟）选修4-4：坐标系与参数方程
在直角坐标平面内，以坐标原点O为极点，沿x轴的正半轴为极轴建立极坐标系．曲线C的极坐标方程是ρ=4cosθ，直线l的参数方程是
x=-3+
3
2
t
y=
1
2
t
（t为参数），M、N分别为曲线C、直线l上的动点，求|MN|的最小值．
（2010•福建模拟）某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作．比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩．假设每个运动员完成每个系列的两个动作的得分是相互独立的．根据赛前训练的统计数据，某运动员完成甲系列和乙系列动作的情况如下表：
表1：甲系列
动作 K动作 D动作
得分 100 80 40 1-
概率
3
4
1
4
3
4
1
4
表2：乙系列
动作 K动作 D动作
得分 90 50 20 0
概率
9
10
1
10
9
10
1
10
现该运动员最后一个出场，之前其他运动员的最高得分为115分
（Ⅰ）若该运动员希望获得该项目的第一名，应选择哪个系列？说明理由，并求其获得第一名的概率；
（Ⅱ）若该运动员选择乙系列，求其成绩ξ的分布列及其数学期望Eξ．
（2010•福建模拟）今有甲、乙、丙、丁四人通过“拔河”进行“体力”较量．当甲、乙两人为一方，丙、丁两人为另一方时，双方势均力敌；当甲与丙对调以后，甲、丁一方轻而易举地战胜了乙、丙一方；而乙凭其一人之力便战胜了甲、丙两人的组合．那么，甲、乙、丙、丁四人的“体力”由强到弱的顺序是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网