摘要：(2)若数列满足.求使对于一切,都成立的的取值集合.
网址：http://m.1010jiajiao.com/timu_id_49217[举报]
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题：（本大题共5个小题，每小题5分，共25分，）
11． 12. 13. 14. 15.
三、解答题：
对于数列{an}，若存在确定的自然数T＞0，使得对任意的自然数n∈N*，都有：an+T=an成立，则称数列{an}是以T为周期的周期数列．
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
)，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．
查看习题详情和答案>>
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
| 1 |
| 2 |
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
| 2009 |
| 2n |
对于数列{an}，若存在确定的自然数T＞0，使得对任意的自然数n∈N*，都有：an+T=an成立，则称数列{an}是以T为周期的周期数列．
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
)，且an+1=-2an2+2an，试判断{an}是否为周期数列，且说明理由；
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
，问是否存在最小的自然数n（n∈N*），使得对一切自然数m≥n，都有bm＞2009？请说明理由．
查看习题详情和答案>>
（1）记Sn=a1+a2+a3+…+an，若{an}满足an+2=an+1-an，且S2=1007，S3=2010，求证：数列{an}是以6为周期的周期数列，并求S2009；
（2）若{an}满足a1=p∈[0，
| 1 |
| 2 |
（3）由（1）得数列{an}，又设数列{bn}，其中bn=an+2n+
| 2009 |
| 2n |
对于数列
{an}，如果存在确定的正整数T，使得an+T＝an对一切正整数n都成立，则称数列{an}是以T为周期的周期数列．若一个周期数列{an}满足an+2＝an+1－an，n∈N+，且a1＝1，a2＝2，求a200，a2009．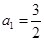
，公差
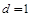，求满足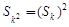
的正整数k；