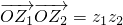摘要:注:①若为复数.则若.则.(×)[为复数.而不是实数]
网址:http://m.1010jiajiao.com/timu_id_491169[举报]
德国数学家在1937年提出了一个著名的猜想:“任给一个正整数n,若n是偶数,则将它减半(即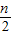 );若n是奇数,则将它乘3加1(即3n+1).不断重复这样的运算,经过有限步后,一定可以得到1”.如6→3→10→5→16→8→4→2→1,如果对正整数n(首项),按上述规则实施变换(注:1可以多次出现)后的第八项为1,那么n的所有可能值共有( )
);若n是奇数,则将它乘3加1(即3n+1).不断重复这样的运算,经过有限步后,一定可以得到1”.如6→3→10→5→16→8→4→2→1,如果对正整数n(首项),按上述规则实施变换(注:1可以多次出现)后的第八项为1,那么n的所有可能值共有( )
A.4个
B.5个
C.6个
D.7个
查看习题详情和答案>>
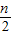 );若n是奇数,则将它乘3加1(即3n+1).不断重复这样的运算,经过有限步后,一定可以得到1”.如6→3→10→5→16→8→4→2→1,如果对正整数n(首项),按上述规则实施变换(注:1可以多次出现)后的第八项为1,那么n的所有可能值共有( )
);若n是奇数,则将它乘3加1(即3n+1).不断重复这样的运算,经过有限步后,一定可以得到1”.如6→3→10→5→16→8→4→2→1,如果对正整数n(首项),按上述规则实施变换(注:1可以多次出现)后的第八项为1,那么n的所有可能值共有( )A.4个
B.5个
C.6个
D.7个
查看习题详情和答案>>
下列命题(为虚数单位)中正确的是
①a,b∈R,若a>b,则a+i>b+i;
②当z是非零实数时,|z+
|≥2恒成立;
③复数z=(1-i)3的实部和虚部都是-2;
④如果|a+2i|<|-2+i|,则实数a的取值范围是-1<a<1;
⑤复数z1,z2与复平面的两个向量
,
相对应,则
•
=z1•z2
其中正确的命题的序号是
查看习题详情和答案>>
①a,b∈R,若a>b,则a+i>b+i;
②当z是非零实数时,|z+
| 1 |
| z |
③复数z=(1-i)3的实部和虚部都是-2;
④如果|a+2i|<|-2+i|,则实数a的取值范围是-1<a<1;
⑤复数z1,z2与复平面的两个向量
| OZ1 |
| OZ2 |
| OZ1 |
| OZ2 |
其中正确的命题的序号是
②③④
②③④
.(注:把你认为正确的命题的序号都填上).下列命题(为虚数单位)中正确的是
①a,b∈R,若a>b,则a+i>b+i;
②当z是非零实数时,|z+
|≥2恒成立;
③复数z=(1-i)3的实部和虚部都是-2;
④如果|a+2i|<|-2+i|,则实数a的取值范围是-1<a<1;
⑤复数z1,z2与复平面的两个向量
,
相对应,则
•
=z1•z2
其中正确的命题的序号是______.(注:把你认为正确的命题的序号都填上).
查看习题详情和答案>>
①a,b∈R,若a>b,则a+i>b+i;
②当z是非零实数时,|z+
| 1 |
| z |
③复数z=(1-i)3的实部和虚部都是-2;
④如果|a+2i|<|-2+i|,则实数a的取值范围是-1<a<1;
⑤复数z1,z2与复平面的两个向量
| OZ1 |
| OZ2 |
| OZ1 |
| OZ2 |
其中正确的命题的序号是______.(注:把你认为正确的命题的序号都填上).
 |≥2恒成立;
|≥2恒成立;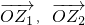 相对应,则
相对应,则