题目内容
下列命题(为虚数单位)中正确的是
①a,b∈R,若a>b,则a+i>b+i;
②当z是非零实数时,|z+ |≥2恒成立;
|≥2恒成立;
③复数z=(1-i)3的实部和虚部都是-2;
④如果|a+2i|<|-2+i|,则实数a的取值范围是-1<a<1;
⑤复数z1,z2与复平面的两个向量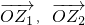 相对应,则
相对应,则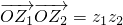
其中正确的命题的序号是________.(注:把你认为正确的命题的序号都填上).
②③④
分析:①复数不能比较大小,故不正确;
②利用基本不等式的性质即可判断出;
③利用复数的运算法则即可化简出;
④利用复数模的计算公式即可得出;
⑤利用向量的数量积的意义和复数乘法的意义即可判断出.
解答:①复数不能比较大小,因此a+i>b+i不正确;
②当z是非零实数时,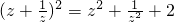
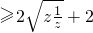 =4,当且仅当z2=1时取等号,∴
=4,当且仅当z2=1时取等号,∴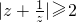 ,故正确;
,故正确;
③z=(1-i)2(1-i)=-2i(1-i)=-2-2i,∴复数z的实部和虚部都是-2,正确;
④如果|a+2i|<|-2+i|,a为实数,则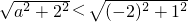 ,化为a2<1,解得-1<a<1,∴实数a的取值范围是-1<a<1,正确;
,化为a2<1,解得-1<a<1,∴实数a的取值范围是-1<a<1,正确;
⑤由向量的数量积可知: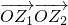 是一个实数;由复数的乘法运算法则可知:z1•z2表示一个复数,因此二者不是一回事,故不正确.
是一个实数;由复数的乘法运算法则可知:z1•z2表示一个复数,因此二者不是一回事,故不正确.
综上可知:只有②③④正确.
故答案为②③④.
点评:熟练掌握复数不能比较大小的性质、复数的运算法则、复数模的计算公式、向量的数量积的意义和复数乘法的意义、基本不等式的性质是解题的关键.
分析:①复数不能比较大小,故不正确;
②利用基本不等式的性质即可判断出;
③利用复数的运算法则即可化简出;
④利用复数模的计算公式即可得出;
⑤利用向量的数量积的意义和复数乘法的意义即可判断出.
解答:①复数不能比较大小,因此a+i>b+i不正确;
②当z是非零实数时,
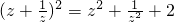
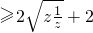 =4,当且仅当z2=1时取等号,∴
=4,当且仅当z2=1时取等号,∴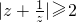 ,故正确;
,故正确;③z=(1-i)2(1-i)=-2i(1-i)=-2-2i,∴复数z的实部和虚部都是-2,正确;
④如果|a+2i|<|-2+i|,a为实数,则
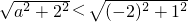 ,化为a2<1,解得-1<a<1,∴实数a的取值范围是-1<a<1,正确;
,化为a2<1,解得-1<a<1,∴实数a的取值范围是-1<a<1,正确;⑤由向量的数量积可知:
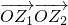 是一个实数;由复数的乘法运算法则可知:z1•z2表示一个复数,因此二者不是一回事,故不正确.
是一个实数;由复数的乘法运算法则可知:z1•z2表示一个复数,因此二者不是一回事,故不正确.综上可知:只有②③④正确.
故答案为②③④.
点评:熟练掌握复数不能比较大小的性质、复数的运算法则、复数模的计算公式、向量的数量积的意义和复数乘法的意义、基本不等式的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 给出下列5个命题:
给出下列5个命题: