摘要：⑤为常数) 高中数学第十四章 导 数考试内容: 导数的背影． 导数的概念． 多项式函数的导数． 利用导数研究函数的单调性和极值．函数的最大值和最小值． 考试要求: (1)了解导数概念的某些实际背景． (2)理解导数的几何意义． (3)掌握函数.y=c的导数公式.会求多项式函数的导数． (4)理解极大值.极小值.最大值.最小值的概念.并会用导数求多项式函数的单调区间.极大值.极小值及闭区间上的最大值和最小值． (5)会利用导数求某些简单实际问题的最大值和最小值．
网址：http://m.1010jiajiao.com/timu_id_491119[举报]
已知等差数列{an}的首项a1=1，公差d＞0，且第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项．
（I）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意正整数n均有
+
+
+…+
=（n+1）an+1成立，其中m为不等于零的常数，求数列{cn}的前n项和Sn．
查看习题详情和答案>>
（I）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意正整数n均有
| c1 |
| b1 |
| c2 |
| mb2 |
| c3 |
| m2b3 |
| cn |
| mn-1bn |
已知等差数列{an}的首项a1=1，公差d＞0，且第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项．
（I）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意正整数n均有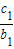
+
+
+…+
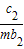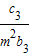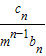=（n+1）an+1成立，其中m为不等于零的常数，求数列{cn}的前n项和Sn．
查看习题详情和答案>>
（I）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意正整数n均有
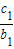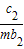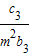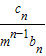+++…+=（n+1）an+1成立，其中m为不等于零的常数，求数列{cn}的前n项和Sn．查看习题详情和答案>>
已知等差数列{an}的首项a1=1，公差d＞0，且第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项．
（I）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意正整数n均有
+
+
+…+
=（n+1）an+1成立，其中m为不等于零的常数，求数列{cn}的前n项和Sn．
查看习题详情和答案>>
（I）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意正整数n均有
+++…+=（n+1）an+1成立，其中m为不等于零的常数，求数列{cn}的前n项和Sn．查看习题详情和答案>>
+
+
+…+
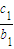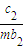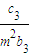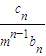=（n+1）an+1成立，其中m为不等于零的常数，求数列{cn}的前n项和Sn．