题目内容
已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项.(I)求数列{an}与{bn}的通项公式;
(Ⅱ)设数列{cn}对任意正整数n均有
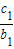 +
+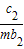 +
+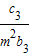 +…+
+…+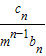 =(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
=(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
【答案】分析:(1)依已知可先求首项和公差,进而求出通项an和bn,在求首项和公差时,主要根据先表示出等差数列的三项,根据这三项是等比数列的三项,且三项成等比数列,用等比中项的关系写出算式,解出结果.
(2)由题先求出{an}的通项公式后再求Sn.仿写一个题目所给的条件,两式相减得到数列{cn}的表达式,讨论当3m=1和当3m≠1两种情况,前一种用等差数列的前n项和公式,后一种情况用错位相减法来解出结果.
解答:解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,整理得2a1d=d2.
∵a1=1,解得d=2(d=0不合题意舍去),
∴an=2n-1
由b2=a2=3,b3=a5=9,
易求得bn=3n-1
(2)当n=1时,c1=6;
当n≥2时,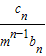 =(n+1)an+1-nan=4n+1,
=(n+1)an+1-nan=4n+1,
∴cn=(4n+1)mn-1bn=(4n+1)(3m)n-1.
∴cn=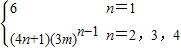
当3m=1,即m= 时,
时,
Sn=6+9+13+…+(4n+1)
=6+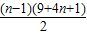
=6+(n-1)(2n+5)=2n2+3n+1.
当3m≠1,即m≠ 时,
时,
Sn=c1+c2++cn,即
Sn=6+9•(3m)+13•(3m)2++(4n-3)(3m)n-2+(4n+1)(3m)n-1.①
3mSn=6•3m+9•(3m)2+13•(3m)3++(4n-3)(3m)n-1+(4n+1)(3m)n.②
①-②得
(1-3m)Sn=6+3•3m+4•(3m)2+4•(3m)3++4•(3m)n-1-(4n+1)(3m)n
=6+9m+4[(3m)2+(3m)3++(3m)n-1]-(4n+1)(3m)n
=6+9m+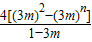 -(4n+1)(3m)n.
-(4n+1)(3m)n.
∴Sn=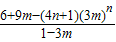 +
+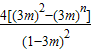 .
.
∴Sn=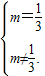
点评:本题主要考查了数列的基本知识和解决数列问题的基本方法,如基本量法,错位相减求和法等.本题是一个综合题,若在高考题中出现时,应该是一个合格的题目.
(2)由题先求出{an}的通项公式后再求Sn.仿写一个题目所给的条件,两式相减得到数列{cn}的表达式,讨论当3m=1和当3m≠1两种情况,前一种用等差数列的前n项和公式,后一种情况用错位相减法来解出结果.
解答:解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,整理得2a1d=d2.
∵a1=1,解得d=2(d=0不合题意舍去),
∴an=2n-1
由b2=a2=3,b3=a5=9,
易求得bn=3n-1
(2)当n=1时,c1=6;
当n≥2时,
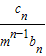 =(n+1)an+1-nan=4n+1,
=(n+1)an+1-nan=4n+1,∴cn=(4n+1)mn-1bn=(4n+1)(3m)n-1.
∴cn=
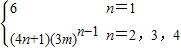
当3m=1,即m=
 时,
时,Sn=6+9+13+…+(4n+1)
=6+
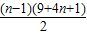
=6+(n-1)(2n+5)=2n2+3n+1.
当3m≠1,即m≠
 时,
时,Sn=c1+c2++cn,即
Sn=6+9•(3m)+13•(3m)2++(4n-3)(3m)n-2+(4n+1)(3m)n-1.①
3mSn=6•3m+9•(3m)2+13•(3m)3++(4n-3)(3m)n-1+(4n+1)(3m)n.②
①-②得
(1-3m)Sn=6+3•3m+4•(3m)2+4•(3m)3++4•(3m)n-1-(4n+1)(3m)n
=6+9m+4[(3m)2+(3m)3++(3m)n-1]-(4n+1)(3m)n
=6+9m+
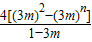 -(4n+1)(3m)n.
-(4n+1)(3m)n.∴Sn=
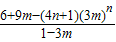 +
+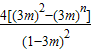 .
.∴Sn=
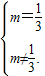
点评:本题主要考查了数列的基本知识和解决数列问题的基本方法,如基本量法,错位相减求和法等.本题是一个综合题,若在高考题中出现时,应该是一个合格的题目.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.