摘要：⑵第二数学归纳法:设是一个与正整数有关的命题.如果
网址：http://m.1010jiajiao.com/timu_id_491070[举报]
设f（x）是非负值函数，对于x1，x2≥0，有等式f（x1+x2）=f（x1）+f（x2）+2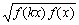
，求证：f（nx）=n2f （x）（n∈N*）.
，求证：f（nx）=n分析：所求证的函数等式是一个与正整数n有关的命题，而题设所给的条件又是一种递推关系，所以可以考虑用数学归纳法证明.
查看习题详情和答案>>灌满开水的热水瓶上瓶盖放在室内，如果瓶内开水原来的温度是θ1度，室内气温是θ0度，t分钟后，开水的温度可由公式θ=θ0＋（θ1-θ0）e-kt求得，这里，k是一个与热水瓶类型有关的正的常量.现有一只某种类型的热水瓶，测得瓶内水温为100℃，过1小时后又测得瓶内水温变为98℃.已知某种奶粉必须用不低于85℃的开水冲调，现用这种类型的热水瓶在早上六点灌满100℃的开水，问：能否在这一天的中午十二点用这瓶开水来冲调上述奶粉？（假定该地白天室温为20℃）
查看习题详情和答案>>
灌满开水的热水瓶放在室内，如果瓶内开水原来的温度是θ1度，室内气温是θ0度，t分钟后，开水的温度可由公式θ=θ0＋(θ1-θ0)e-kt求得，这里，k是一个与热水瓶类型有关的正的常量.现有一只某种类型的热水瓶，测得瓶内水温为100 ℃，过1小时后又测得瓶内水温变为98 ℃.已知某种奶粉必须用不低于85 ℃的开水冲调，现用这种类型的热水瓶在早上六点灌满100 ℃的开水，问：能否在这一天的中午十二点用这瓶开水来冲调上述奶粉？(假定该地白天室温为20 ℃)
查看习题详情和答案>>
某个与正整数有关的命题,若当n=k(k∈N*)时,该命题成立,则可推出当n=k+1时,该命题也成立,现已知当n=5时,该命题不成立,那么可能
A.当n=6时,该命题成立 B.当n=4时,该命题不成立
C.当n=6时,该命题不成立 D.当n=4时,该命题成立
查看习题详情和答案>>设α是一个任意角，它的终边与单位圆交于点P（x，y），由此定义了正弦（sinα）、余弦（cosα）、正切（tanα），其实还有另外三个三角函数，分别是：余切（cotα=
）、正割（secα=
）、余割（cscα=
）．则下列关系式错误的是（ ）
| x |
| y |
| 1 |
| x |
| 1 |
| y |
A、cotα=
| ||
B、secα=
| ||
C、cscα=
| ||
| D、cot2α-csc2α=1 |