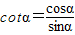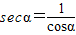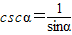题目内容
设α是一个任意角,它的终边与单位圆交于点P(x,y),由此定义了正弦(sinα)、余弦(cosα)、正切(tanα),其实还有另外三个三角函数,分别是:余切(cotα=
)、正割(secα=
)、余割(cscα=
).则下列关系式错误的是( )
| x |
| y |
| 1 |
| x |
| 1 |
| y |
A、cotα=
| ||
B、secα=
| ||
C、cscα=
| ||
| D、cot2α-csc2α=1 |
分析:根据三角函数定义,分别表示出正弦、余弦、余切、余割代入每一选项中的左边和右边,即可得到正确的选项及错误的选项,得出本题的答案.
解答:解:根据三角形函数定义得:sinα=y,cosα=x,
A、∵cotα=
,
=
,∴cotα=
,本选项正确;
B、secα=
,又cosα=x,∴
=
,则secα=
,本选项正确;
C、cscα=
,又sinα=y,∴
=
,则cscα=
,本选项正确;
D、∵x2+y2=1,即x2-1=-y2,
∴cot2α-csc2α=(
)2-(
)2=
=-1,本选项错误,
故选D
A、∵cotα=
| x |
| y |
| cosα |
| sinα |
| x |
| y |
| cosα |
| sinα |
B、secα=
| 1 |
| x |
| 1 |
| cosα |
| 1 |
| x |
| 1 |
| cosα |
C、cscα=
| 1 |
| y |
| 1 |
| sinα |
| 1 |
| y |
| 1 |
| sinα |
D、∵x2+y2=1,即x2-1=-y2,
∴cot2α-csc2α=(
| x |
| y |
| 1 |
| y |
| x2-1 |
| y2 |
故选D
点评:此题考查了同角三角函数间的基本关系,以及三角函数的定义,熟练掌握三角函数定义是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
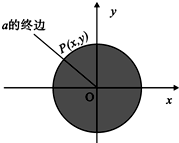 如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),我们把
如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),我们把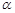 是一个任意角,它的终边与单位圆交于点
是一个任意角,它的终边与单位圆交于点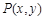 ,我们把
,我们把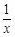 叫做
叫做 ;把
;把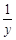 叫做
叫做 . 则
. 则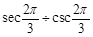 =
=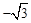 B.
B. 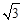 C.
C. 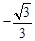 D.
D. 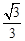
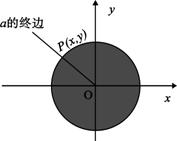
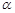 是一个任意角,它的终边与单位圆交于点
是一个任意角,它的终边与单位圆交于点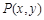 ,由此定义了正弦(
,由此定义了正弦(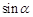 )、余弦(
)、余弦(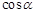 )、正切(
)、正切(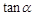 ),其实还有另外三个三角函数,分别是:余切(
),其实还有另外三个三角函数,分别是:余切(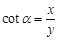 )、正割(
)、正割(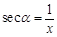 )、余割(
)、余割(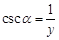 ). 则下列关系式错误的是( )
). 则下列关系式错误的是( )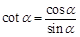 B.
B.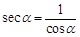 C.
C.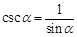 D.
D.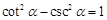
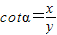 )、正割(
)、正割(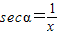 )、余割(
)、余割(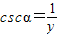 ).则下列关系式错误的是( )
).则下列关系式错误的是( )