摘要：空间距离的求法(1)两异面直线间的距离.高考要求是给出公垂线.所以一般先利用垂直作出公垂线.然后再进行计算,(2)求点到直线的距离.一般用三垂线定理作出垂线再求解,(3)求点到平面的距离.一是用垂面法.借助面面垂直的性质来作.因此.确定已知面的垂面是关键,二是不作出公垂线.转化为求三棱锥的高.利用等体积法列方程求解,
网址：http://m.1010jiajiao.com/timu_id_490914[举报]
给出以下几个命题：
①已知函数f(x)=
则f（x）=x有三个根；
②?x0∈R，x0≤sinx0；
③过空间任一点，有且只有一个平面与两异面直线同时平行；
④两条直线l1：A1x+B1y+C1=0与直线l2：A2x+B2y+C2=0平行的充要条件是
⑤y=
的定义域是[2，+∞）．
则正确的命题有 （填序号）．
查看习题详情和答案>>
①已知函数f(x)=
|
|
②?x0∈R，x0≤sinx0；
③过空间任一点，有且只有一个平面与两异面直线同时平行；
④两条直线l1：A1x+B1y+C1=0与直线l2：A2x+B2y+C2=0平行的充要条件是
|
⑤y=
log
|
则正确的命题有
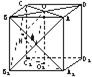如图，在棱长为a的正方体ABCD-A1B1C1D1中，M、O、O1分别是A1B、AC、A1C1的中点，且OH⊥O1B，垂足为H．（1）求证：MO∥平面BB1C1C；
（2）分别求MO与OH的长；
（3）MO与OH是否为异面直线A1B与AC的公垂线？为什么？求这两条异面直线间的距离． 查看习题详情和答案>>
、
，直线a、b，若
，
，则
；