摘要：则①.②.③ ①②③得.注:S为任意多边形的面积(可分别多个三角形的方法).⑵棱锥具有的性质:①正棱锥各侧棱相等.各侧面都是全等的等腰三角形.各等腰三角形底边上的高相等.②正棱锥的高.斜高和斜高在底面内的射影组成一个直角三角形.正棱锥的高.侧棱.侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等.则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等.则顶点在底面上的射影为底面多边形的外心.③棱锥的各侧面与底面所成角均相等.则顶点在底面上的射影为底面多边形内心.④棱锥的顶点到底面各边距离相等.则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直.则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直.则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球.球心0是各条棱的中垂面的交点.此点到各顶点的距离等于球半径,
网址：http://m.1010jiajiao.com/timu_id_490851[举报]
已知一列非零向量
满足：
=(x1，y1)，
=(xn，yn)=
(xn-1-yn-1，xn-1+yn-1)(n≥2)．
（Ⅰ）证明：{|
|}是等比数列；
（Ⅱ）求向量
n-1与
n的夹角(n≥2)；
（Ⅲ）设
1=(1，2)，把
，
，…，
，…中所有与
共线的向量按原来的顺序排成一列，记为
，
，…，
，…，令
n=
+
+…+
，0为坐标原点，求点列{Bn}的极限点B的坐标．
（注：若点Bn坐标为(tn，sn)，且
tn=t，
sn=s，则称点B(t，s)为点列{Bn}的极限点．）
查看习题详情和答案>>
| an |
| a1 |
| an |
| 1 |
| 2 |
（Ⅰ）证明：{|
| an |
（Ⅱ）求向量
| a |
| a |
（Ⅲ）设
| a |
| a1 |
| a2 |
| an |
| a1 |
| b1 |
| b2 |
. |
| bn |
| OB |
| b1 |
| b2 |
| bn |
（注：若点Bn坐标为(tn，sn)，且
| lim |
| n→∞ |
| lim |
| n→∞ |
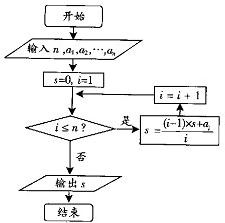随机抽取某产品m件，测得其长度分别为k（k∈R），则如图所示的程序框图输出的S=