摘要:证明:因为所以.所以.结论!
网址:http://m.1010jiajiao.com/timu_id_490515[举报]
若a>b>c,则
+
≥
证明:因为(a-c)(
+
)=(a-b+b-c)(
+
)=2+
+
∵a>b>c∴a-b>0,b-c>0;
∴
+
≥2
=2
∴2+
+
≥4∴(a-c)(
+
)≥4
因为a>c所以a-c>0
所以
+
≥
类比上述命题及证明思路,回答以下问题:
①若a>b>c>d,比较
+
+
与
的大小,并证明你的猜想;
②若a>b>c>d>e,且
+
+
+
≥
恒成立,试猜想m的最大值,并写出猜想过程,不要求证明.
查看习题详情和答案>>
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
证明:因为(a-c)(
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| a-b |
| 1 |
| b-c |
| b-c |
| a-b |
| a-b |
| b-c |
∵a>b>c∴a-b>0,b-c>0;
∴
| b-c |
| a-b |
| a-b |
| b-c |
|
∴2+
| b-c |
| a-b |
| a-b |
| b-c |
| 1 |
| a-b |
| 1 |
| b-c |
因为a>c所以a-c>0
所以
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
类比上述命题及证明思路,回答以下问题:
①若a>b>c>d,比较
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-d |
| 9 |
| a-d |
②若a>b>c>d>e,且
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-d |
| 1 |
| d-e |
| m |
| a-e |
如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .
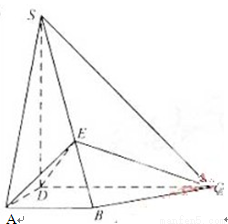
【解析】本试题主要考查了立体几何中的运用。
(1)证明:因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.,因此可知得到平面EDC⊥平面SBC.
(Ⅱ)由SA2= SD2+AD2 = 5 ,AB=1,SE=2EB,AB⊥SA,知
AE2= (1 /3 SA)2+(2/ 3 AB)2 =1,又AD=1.
故△ADE为等腰三角形.
取ED中点F,连接AF,则AF⊥DE,AF2= AD2-DF2 =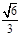 .
.
连接FG,则FG∥EC,FG⊥DE.
所以,∠AFG是二面角A-DE-C的平面角.
连接AG,AG= 2 ,FG2= DG2-DF2
=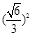 ,
,
cos∠AFG=(AF2+FG2-AG2 )/2⋅AF⋅FG =-1 /2 ,
所以,二面角A-DE-C的大小为120°
查看习题详情和答案>>
 ,有下列命题:
,有下列命题: 轴对称;
轴对称; 时,
时, 是增函数,当
是增函数,当 时,
时, ;
; )上是增函数;
)上是增函数;