题目内容
用数学归纳法证明等式对所以n∈N*均成立．
同解析
解析:
i)当n=1时，左式=
，右式=
， ∴ 左式=右式，等式成立．
ii)假设当n=k(k∈N)时等式成立，
即
，
则当n=k+1时，
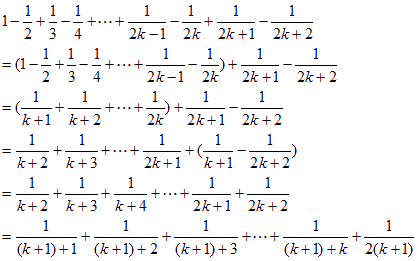
即n=k+1时，等式也成立，
由i) ii)可知，等式对n∈N均成立．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
解析:
鹰派教辅衔接教材河北教育出版社系列答案初中暑期衔接系列答案题目内容
用数学归纳法证明等式对所以n∈N*均成立．
同解析
i)当n=1时，左式=，右式=， ∴ 左式=右式，等式成立．
ii)假设当n=k(k∈N)时等式成立，
即，
则当n=k+1时，
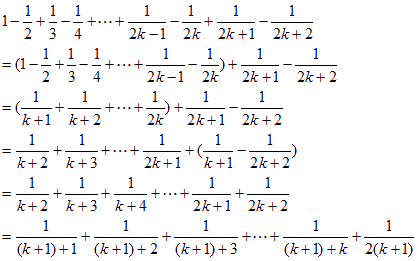
即n=k+1时，等式也成立，
由i) ii)可知，等式对n∈N均成立．
鹰派教辅衔接教材河北教育出版社系列答案初中暑期衔接系列答案