摘要:.推广:性质1
网址:http://m.1010jiajiao.com/timu_id_490269[举报]
已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在(0,
,那么该函数在(0,![]() )上减函数,在
)上减函数,在![]() 是增函数。
是增函数。
(1)如果函数![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(2)研究函数![]() (常数
(常数![]() )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;
(3)对函数![]() 和
和![]() (常数
(常数![]() )作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
![]() (n是正整数)在区间[
(n是正整数)在区间[![]() ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。
已知函数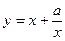 有如下性质:如果常数
有如下性质:如果常数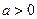 ,那么该函数在(0,
,那么该函数在(0,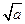 )上减函数,在
)上减函数,在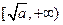 是增函数。
是增函数。
(1)如果函数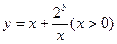 的值域为
的值域为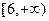 ,求
,求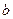 的值;
的值;
(2)研究函数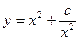 (常数
(常数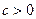 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;
(3)对函数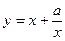 和
和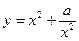 (常数
(常数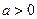 )作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
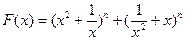 (n是正整数)在区间[
(n是正整数)在区间[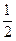 ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。
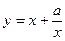 有如下性质:如果常数
有如下性质:如果常数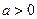 ,那么该函数在(0,
,那么该函数在(0,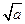 )上减函数,在
)上减函数,在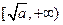 是增函数。
是增函数。(1)如果函数
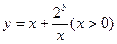 的值域为
的值域为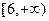 ,求
,求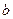 的值;
的值;(2)研究函数
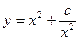 (常数
(常数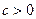 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;(3)对函数
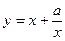 和
和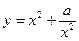 (常数
(常数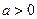 )作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例。研究推广后的函数的单调性(只须写出结论,不必证明),并求函数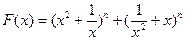 (n是正整数)在区间[
(n是正整数)在区间[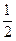 ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。 规定
且
(1)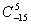 的值;
的值;
(2)组合数的两个性质: ;
; 是否都能推广到
是否都能推广到 的情形?若能推广,则写出推广的形式并给予证明,或不能则说明理由;
的情形?若能推广,则写出推广的形式并给予证明,或不能则说明理由;
(3)已知组合数 是正整数,证明:当
是正整数,证明:当 是正整数时,
是正整数时, 。
。
查看习题详情和答案>>
规定![]() ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且![]() =1,这是组合数
=1,这是组合数![]() (n、m是正整数,且m≤n)的一种推广。
(n、m是正整数,且m≤n)的一种推广。
(I)求![]() 的值。
的值。
(II)组合数的两个性质;①![]() ;②
;②![]() 。是否都能推广到
。是否都能推广到![]() (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由;
 ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且 =1,这是组合数
=1,这是组合数 (n,m是正整数,且m≤n)的一种推广,
(n,m是正整数,且m≤n)的一种推广,  的值;
的值; 取得最小值?
取得最小值?  ;②
;② ,
, (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由。
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由。