题目内容
规定 ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且 =1,这是组合数
=1,这是组合数 (n,m是正整数,且m≤n)的一种推广,
(n,m是正整数,且m≤n)的一种推广,
(1)求 的值;
的值;
(2)设x>0,当x为何值时, 取得最小值?
取得最小值?
(3)组合数的两个性质:① ;②
;② ,
,
是否都能推广到 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由。
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由。
解:(1)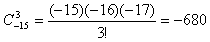 ;
;
(2)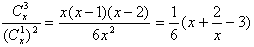 ,
,
因为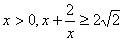 ,
,
当且仅当 时,等号成立,
时,等号成立,
∴当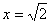 时,
时,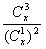 取得最小值。
取得最小值。
(3)性质(1)不能推广。 例如当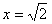 时,
时,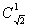 有定义,但
有定义,但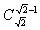 无意义;
无意义;
性质(2)能推广,它的推广形式是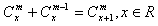 ,m是正整数,
,m是正整数,
事实上
当m=1时,有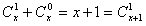 ;
;
当m≥2时,
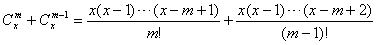
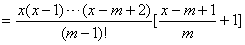
 ,
,
[证明](3)当x≥m时,组合数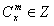 ,
,
当0≤x<m时,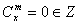 ,
,
当x<0时,∵-x+m-1>0,
∴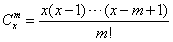
 。
。
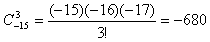 ;
;(2)
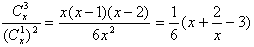 ,
,因为
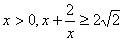 ,
,当且仅当
 时,等号成立,
时,等号成立,∴当
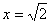 时,
时,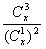 取得最小值。
取得最小值。(3)性质(1)不能推广。 例如当
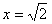 时,
时,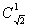 有定义,但
有定义,但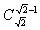 无意义;
无意义;性质(2)能推广,它的推广形式是
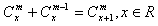 ,m是正整数,
,m是正整数,事实上
当m=1时,有
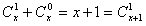 ;
;当m≥2时,
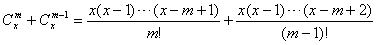
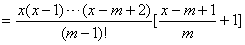
 ,
,[证明](3)当x≥m时,组合数
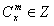 ,
,当0≤x<m时,
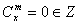 ,
,当x<0时,∵-x+m-1>0,
∴
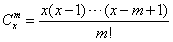
 。
。
练习册系列答案
相关题目
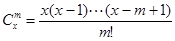 ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且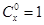 ,这是组合数
,这是组合数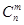 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.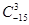 的值;
的值;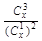 取得最小值?
取得最小值?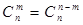 . ②
. ②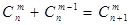 .
.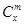 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由. ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且 ,这是组合数
,这是组合数 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广. 的值;
的值; 取得最小值?
取得最小值? . ②
. ② .
. (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由. ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且 ,这是组合数
,这是组合数 (n,m是正整数,且m≤n)的一种推广,
(n,m是正整数,且m≤n)的一种推广, 的值;
的值; ;②
;② ,
, (x∈R,m是正整数)的情形?若能推广,请写出推广的形式,并给出明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,请写出推广的形式,并给出明;若不能,则说明理由;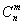 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时, ∈Z。
∈Z。