网址:http://m.1010jiajiao.com/timu_id_489396[举报]
1. B 解析:由图可知AB、BC、CD的距离分别是%20物理图象、方法技巧、物理题型.files/image272.gif) 得,
得,%20物理图象、方法技巧、物理题型.files/image274.gif) ,所以光源应满足的条件是间歇发光其间隔时间为0.14s。
,所以光源应满足的条件是间歇发光其间隔时间为0.14s。
2. C 解析:依题意作出物体的v-t图象,如图1所示。图线下方所围成的面积表示物体的位移,由几何知识知图线②、③不满足AB=BC。只能是①这种情况。因为斜率表示加速度,所以a1<a2,选项C正确。
%20物理图象、方法技巧、物理题型.files/image276.jpg)
%20物理图象、方法技巧、物理题型.files/image277.gif) 3. D 解析:对挂钩进行受力分析,如图所示,图中α、β为A、B绳与竖直方向的夹角,两绳拉力如图中FA0、FB0所示;当右侧杆向左平移,则α、β均变小,两绳拉力如图中FA、FB所示;由图可知,A、B绳的拉力均变小,AB错;由于挂钩受力平衡,两绳对挂钩的拉力合力一定与衣服对挂钩的拉力大小相等、方向相反,因此合力不变,D正确。
3. D 解析:对挂钩进行受力分析,如图所示,图中α、β为A、B绳与竖直方向的夹角,两绳拉力如图中FA0、FB0所示;当右侧杆向左平移,则α、β均变小,两绳拉力如图中FA、FB所示;由图可知,A、B绳的拉力均变小,AB错;由于挂钩受力平衡,两绳对挂钩的拉力合力一定与衣服对挂钩的拉力大小相等、方向相反,因此合力不变,D正确。
4. A 解析:从0到%20物理图象、方法技巧、物理题型.files/image279.gif) 的时间内,磁感应强度从2
的时间内,磁感应强度从2%20物理图象、方法技巧、物理题型.files/image281.gif) 均匀减小到0,根据楞次定律和右手定则可判断出感应电流的方法与规定的方向相反,大小为:
均匀减小到0,根据楞次定律和右手定则可判断出感应电流的方法与规定的方向相反,大小为:%20物理图象、方法技巧、物理题型.files/image283.gif) ;同理,从
;同理,从%20物理图象、方法技巧、物理题型.files/image279.gif) 到T的时间,磁感应强度方向向下,大小均匀增大,感应电流的磁场方向向上,由右手定则可知感应电流的方法与规定的方向相反,大小为:
到T的时间,磁感应强度方向向下,大小均匀增大,感应电流的磁场方向向上,由右手定则可知感应电流的方法与规定的方向相反,大小为:%20物理图象、方法技巧、物理题型.files/image285.gif) ,故A选项正确。
,故A选项正确。
5. ABC 解析:从F-t图象上可以看出,在0~t1、t2~t3和t4以后的时间内,弹簧秤对钩码的拉力F等于钩码的重力10N;t1~t2这段时间内,弹簧秤对钩码的拉力F小于钩码的重力,钩码处于失重状态;t3~t4这段时间内,弹簧秤对钩码的拉力F大于钩码的重力,钩码处于超重状态,所以选项ABC正确。
6. B 解析:由图像的变化快慢可知曲线ab先变化非常快,为斥力图,cd为引力图,e点是两曲线的交点,即分子间引力与斥力相等时,此时分子间距离的数量级为10-
7. C 解析:假设将小球放在弹簧顶端释放球,这就是一个常见的弹簧振子,由对称性知,球到达最低点的加速度为%20物理图象、方法技巧、物理题型.files/image252.gif) ,本题中弹簧在最低点时压缩量比假设的模型大,故答案为C.
,本题中弹簧在最低点时压缩量比假设的模型大,故答案为C.
8. B 解析:导体杆往复运动,切割磁感线相当于电源,其产生的感应电动势E=Blv,由于杆相当于弹簧振子,其在O点处的速度最大,产生的感应电动势最大,因此电路中的电流最大。根据右手定则,电流在P、Q两处改变方向,此时的电流为零。故选择B.
9.
解析:由电源的伏安特性曲线读得电源电动势为E=1.5V,横截距表示短路电流I=%20物理图象、方法技巧、物理题型.files/image287.gif) Ω。
Ω。
a点对应的电源输出电压为1.0V,电流为%20物理图象、方法技巧、物理题型.files/image289.gif) Ω,电源内部热耗功率为
Ω,电源内部热耗功率为%20物理图象、方法技巧、物理题型.files/image291.gif) W。
W。
图线中的b点所对应的外电阻Rb上的电压为0.5V,流过其中的电流为%20物理图象、方法技巧、物理题型.files/image293.gif) Ω 输出功率为Pb=IbUb=0.25W。
Ω 输出功率为Pb=IbUb=0.25W。
%20物理图象、方法技巧、物理题型.files/image295.jpg) 11. 解析:(1)因为电路中需要得到改装后电压表量程与电源电动势两个未知数,所以需要两个电路状态联立方程求解。连接如图所示。
11. 解析:(1)因为电路中需要得到改装后电压表量程与电源电动势两个未知数,所以需要两个电路状态联立方程求解。连接如图所示。
(2)当当S1与S2均闭合时,由闭合电路的欧姆定律得:
%20物理图象、方法技巧、物理题型.files/image297.gif)
即: %20物理图象、方法技巧、物理题型.files/image299.gif) ①
①
当S1闭合,S2断开时,由闭合电路的欧姆定律得:
%20物理图象、方法技巧、物理题型.files/image301.gif) ,
,
即:%20物理图象、方法技巧、物理题型.files/image303.gif) ②
②
由①②两式可得:%20物理图象、方法技巧、物理题型.files/image305.gif) ,
,%20物理图象、方法技巧、物理题型.files/image307.gif)
则电压表的量程:%20物理图象、方法技巧、物理题型.files/image309.gif)
12. 解析:用图象求解,做出速度时间图象如图所示,从图象看出从B上升到最高点的时间与由最高点落回A的时间之比为1:2,所以从A运动到B的时间与从B上升到最高点的时间之比为1:3,即%20物理图象、方法技巧、物理题型.files/image311.gif) ,又
,又%20物理图象、方法技巧、物理题型.files/image313.gif)
%20物理图象、方法技巧、物理题型.files/image315.gif) 所以解得
所以解得%20物理图象、方法技巧、物理题型.files/image317.gif)
%20物理图象、方法技巧、物理题型.files/image319.jpg)
13.
半径/cm
质量/m0
角速度/rad?s-1
圈数
转动动能/J
6.4
14.4
25.6
12.8
19.2
25.6
25.6
57.6
102.4
(2)EK = kmω2 r2 (k是比例常数) (3)控制变量法
14. 解析:(1)依题意分析可知:碰撞发生在第1、2两次闪光时刻之间,碰撞后B静止,故碰撞发生在x=
(2)碰撞后A向左做匀速直线运动,设其速度为%20物理图象、方法技巧、物理题型.files/image321.gif) ,
,%20物理图象、方法技巧、物理题型.files/image323.gif)
碰撞到第二次闪光时A向左运动%20物理图象、方法技巧、物理题型.files/image325.gif) ,有
,有%20物理图象、方法技巧、物理题型.files/image327.gif)
第一次闪光到发生碰撞时间为%20物理图象、方法技巧、物理题型.files/image329.gif) ,有:
,有:%20物理图象、方法技巧、物理题型.files/image331.gif)
由以上各式可得:%20物理图象、方法技巧、物理题型.files/image333.gif)
(3)取向右方向为正方向,碰撞前:A的速度%20物理图象、方法技巧、物理题型.files/image335.gif) ,B的速度
,B的速度%20物理图象、方法技巧、物理题型.files/image337.gif)
碰撞后:A的速度%20物理图象、方法技巧、物理题型.files/image339.gif) ,B的速度
,B的速度%20物理图象、方法技巧、物理题型.files/image341.gif)
由动量守恒守恒定律可得:%20物理图象、方法技巧、物理题型.files/image343.gif)
由以上各式可得:%20物理图象、方法技巧、物理题型.files/image345.gif) :
:%20物理图象、方法技巧、物理题型.files/image347.gif) =2:3
=2:3
(1)那么摆球直径为
(2)单摆摆长是
(3)如果测定了若干次全振动的时间如图3秒表所示,那么秒表读数是
(4)某同学用该实验装置测当地重力加速度,若他测得的g值偏大,可能的原因是
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将50次全振动数为49次

(5)为提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L与T的数据,再以L为横坐标、T2为纵坐标将所得数据拟合成直线,并求得该直线的斜率K.则重力加速度g=
(1)那么单摆摆长是
(2)如果测定了40次全振动的时间如图2中秒表所示,那么秒表读数是
 (3)某同学用该实验装置测当地重力加速度,若他测得的g值偏大,可能的原因是
(3)某同学用该实验装置测当地重力加速度,若他测得的g值偏大,可能的原因是A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将50次全振动数为49次
(4)为提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L与T的数据,再以L为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率K.则重力加速度g=
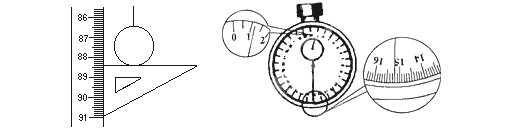
在做“探究单摆周期与摆长的关系”的实验时,如果已知摆球直径为2.00cm,让刻度尺的零点对准摆线的悬点,摆线竖直下垂,如左图所示,
(1)那么单摆摆长是______m.
(2)如果测定了40次全振动的时间如右图中秒表所示,那么秒表读数是______s, 单摆的摆动周期是______s.
(3)某同学用该实验装置测当地重力加速度,若他测得的g值偏大,可能的原因是( )
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将50次全振动数为49次
(4)为提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组 对应的L与T的数据,再以L为横坐标、T2为纵坐标将所得数据连成直线,并求 得该直线的斜率K。则重力加速度g = 。(用K及常数![]() 表示)
表示)

(1)若用刻度尺测出遮光条的宽度d如图乙所示,则d=
(2)实验中可近似认为细线对小车的拉力与重物重力大小相等,则重物的质量m与小车的质量M间应满足的关系为
(3)测出多组重物的质量m和对应遮光条通过B点的时间△t,并算出遮光条通过B点位置时小车的速度v,通过描点作出线性图象,研究小车加速度与力的关系.处理数据时应作出
| 2gLAB |
| M |
| 2gLAB |
| M |
