分组	频数	频率
（3.9，4.2]	4	0.08
（4.2，4.5]	5	0.10
（4.5，4.8]	25	m
（4.8，5.1]	x	y
（5.1，5.4]	6	0.12
合计	n	1.00

为了解我市高三学生的视力状况，绵阳市某医疗卫生机构于2011年9月对某校高三学生进行了一次随机抽样调查．已知该校高三的男女生人数的比例为4：1，调查时根据性别采用分层抽样的方式随机抽取了一部分学生作为样本．现将调查结果分组，分组区间为（3.9，4.2]，（4.2，4.5]，…（5.1，5.4]．经过数据处理，得到如频率分布表：
（1）求频率分布表中未知量x，y，m，n的值；
（2）从样本中视力在（4.2，4.5]和（5.1，5.4]的所有同学中随机抽取两人，求两人的视力差的绝对值低于0.5的概率；
（3）若该校某位高三女生被抽进本次调查的样本的概率为

1

13

，请你根据本次抽样调查的结果估计该校高三学生中视力高于4.8的人数．

已知：向量

m

=(sinx，

3

4

)，

n

=(cosx，-1)，设函数f(x)=2(

m

+

n

)•

n

（1）求f（x）解析式；
（2）在△ABC中，内角A，B，C的对边分别为a，b，c．若a=

3

，b=2，sinB=

6

3

，求f(x)+4cos(2A+

π

6

) (x∈[0，

π

2

])的取值范围．

已知函数f(x)=

|x+m-1|

x-2

，m＞0且f（1）=-1．
（1）求实数m的值；
（2）判断函数y=f（x）在区间（-∞，m-1]上的单调性，并用函数单调性的定义证明；
（3）求实数k的取值范围，使得关于x的方程f（x）=kx分别为：
①有且仅有一个实数解；
②有两个不同的实数解；
③有三个不同的实数解．

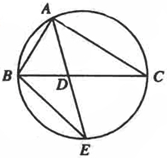
选作题：考生任选一题作答，如果多做，则按所做的第一题计分．
A 如图，△ABC的角平分线AD的延长线交它的外接圆于点E．
（I）证明：△ABE∽△ADC
（II）若△ABC的面积S=

1

2

AD•AE，求∠BAC的大小．
B 已知曲线C₁：

x=-4+cost y=3+sint

（t为参数），C₂：

x=8cosθ y=3sinθ

（θ为参数）．
（1）化C₁，C₂的方程为普通方程，并说明它们分别表示什么曲线；
（2）若C₁上的点P对应的参数为t=

π

2

，Q为C₂上的动点，求PQ中点M到直线C3：

x=3+2t y=-2+t

（t为参数）距离的最小值．                
C 已知函数f（x）=|x-a|．
（Ⅰ）若不等式f（x）≤3的解集为{x|-1≤x≤5}，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若f（x）+f（x+5）≥m对一切实数x恒成立，求实数m的取值范围．