题目内容
 选作题:考生任选一题作答,如果多做,则按所做的第一题计分.
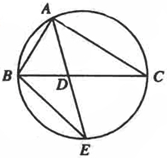
选作题:考生任选一题作答,如果多做,则按所做的第一题计分.A 如图,△ABC的角平分线AD的延长线交它的外接圆于点E.
(I)证明:△ABE∽△ADC
(II)若△ABC的面积S=
| 1 |
| 2 |
B 已知曲线C1:
|
|
(1)化C1,C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C1上的点P对应的参数为t=
| π |
| 2 |
|
C 已知函数f(x)=|x-a|.
(Ⅰ)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
分析:A(Ⅰ)要判断两个三角形相似,可以根据三角形相似判定定理进行证明,但注意观察已知条件中给出的是角的关系,故采用判定定理1更合适,故需要再找到一组对应角相等,由圆周角定理,易得满足条件的角.
(Ⅱ)根据(Ⅰ)的结论,我们可得三角形对应对成比例,由此我们可以将△ABC的面积S=
AD•AE转化为S=
AB•AC,再结合三角形面积公式,不难得到∠BAC的大小.
B(1)分别消去两曲线参数方程中的参数得到两曲线的普通方程,即可得到曲线C1表示一个圆;曲线C2表示一个椭圆;
(2)把t的值代入曲线C1的参数方程得点P的坐标,然后把直线的参数方程化为普通方程,根据曲线C2的参数方程设出Q的坐标,利用中点坐标公式表示出M的坐标,利用点到直线的距离公式表示出M到已知直线的距离,利用两角差的正弦函数公式化简后,利用正弦函数的值域即可得到距离的最小值.
C(Ⅰ)由f(x)=|x-a|,不等式f(x)≤3的解集为{x|-1≤x≤5},知|x-a|≤3的解集为{x|-1≤x≤5},由此能求出a.
(Ⅱ)由(Ⅰ)知,f(x)+f(x+5)≥m对一切实数x恒成立,等价于|x-2|+|x+3|≥m对一切实数x恒成立.由此能求出实数m的取值范围.
(Ⅱ)根据(Ⅰ)的结论,我们可得三角形对应对成比例,由此我们可以将△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
B(1)分别消去两曲线参数方程中的参数得到两曲线的普通方程,即可得到曲线C1表示一个圆;曲线C2表示一个椭圆;
(2)把t的值代入曲线C1的参数方程得点P的坐标,然后把直线的参数方程化为普通方程,根据曲线C2的参数方程设出Q的坐标,利用中点坐标公式表示出M的坐标,利用点到直线的距离公式表示出M到已知直线的距离,利用两角差的正弦函数公式化简后,利用正弦函数的值域即可得到距离的最小值.
C(Ⅰ)由f(x)=|x-a|,不等式f(x)≤3的解集为{x|-1≤x≤5},知|x-a|≤3的解集为{x|-1≤x≤5},由此能求出a.
(Ⅱ)由(Ⅰ)知,f(x)+f(x+5)≥m对一切实数x恒成立,等价于|x-2|+|x+3|≥m对一切实数x恒成立.由此能求出实数m的取值范围.
解答:A(Ⅰ)证明:由已知△ABC的角平分线为AD,
可得∠BAE=∠CAD
因为∠AEB与∠ACB是同弧上的圆周角,
所以∠AEB=∠ACD
故△ABE∽△ADC.
解:(Ⅱ)因为△ABE∽△ADC,
所以
=
,
即AB•AC=AD•AE.
又S=
AB•ACsin∠BAC,
且S=
AD•AE,
故AB•ACsin∠BAC=AD•AE.
则sin∠BAC=1,
又∠BAC为三角形内角,
所以∠BAC=90°.
B解:(1)把曲线C1:
(t为参数)化为普通方程得:(x+4)2+(y-3)2=1,
所以此曲线表示的曲线为圆心(-4,3),半径1的圆;
把C2:
(θ为参数)化为普通方程得:
+
=1,
所以此曲线方程表述的曲线为中心是坐标原点,焦点在x轴上,长半轴为8,短半轴为3的椭圆;
(2)把t=
代入到曲线C1的参数方程得:P(-4,4),
把直线C3:
(t为参数)化为普通方程得:x-2y-7=0,
设Q的坐标为Q(8cosθ,3sinθ),故M(-2+4cosθ,2+
sinθ)
所以M到直线的距离d=
=
,(其中sinα=
,cosα=
)
从而当cosθ=
,sinθ=-
时,d取得最小值
.
C解:(Ⅰ)∵f(x)=|x-a|,不等式f(x)≤3的解集为{x|-1≤x≤5},
∴|x-a|≤3的解集为{x|-1≤x≤5},
∵由|x-a|≤3,解得a-3≤x≤a+3,
∴
,解得a=2.
(Ⅱ)由(Ⅰ)知,f(x)=|x-2|,
∵f(x)+f(x+5)≥m对一切实数x恒成立,
∴|x-2|+|x+3|≥m对一切实数x恒成立.
设y=|x-2|+|x+3|,
由x-2=0,得x=2;由x+3=0,得x=-3.
①当x≥2时,y=x-2+x+3=2x+1≥5;
②当-3≤x<2时,y=2-x+x+3=5;
③当x<-3时,y=2-x-x-3=-2x-1>5.
综上所述,y=|x-2|+|x+3|≥5.
∴若f(x)+f(x+5)≥m对一切实数x恒成立,则m≤5.
故实数m的取值范围是(-∞,5].

可得∠BAE=∠CAD
因为∠AEB与∠ACB是同弧上的圆周角,
所以∠AEB=∠ACD
故△ABE∽△ADC.
解:(Ⅱ)因为△ABE∽△ADC,
所以
| AB |
| AE |
| AD |
| AC |
即AB•AC=AD•AE.
又S=
| 1 |
| 2 |
且S=
| 1 |
| 2 |
故AB•ACsin∠BAC=AD•AE.
则sin∠BAC=1,
又∠BAC为三角形内角,
所以∠BAC=90°.
B解:(1)把曲线C1:
|
所以此曲线表示的曲线为圆心(-4,3),半径1的圆;
把C2:
|
| x2 |
| 64 |
| y2 |
| 9 |
所以此曲线方程表述的曲线为中心是坐标原点,焦点在x轴上,长半轴为8,短半轴为3的椭圆;
(2)把t=
| π |
| 2 |
把直线C3:
|
设Q的坐标为Q(8cosθ,3sinθ),故M(-2+4cosθ,2+
| 3 |
| 2 |
所以M到直线的距离d=
| |4cosθ-3sinθ-13| | ||
|
| |5sin(α-θ)-13| | ||
|
| 4 |
| 5 |
| 3 |
| 5 |
从而当cosθ=
| 4 |
| 5 |
| 3 |
| 5 |
8
| ||
| 5 |
C解:(Ⅰ)∵f(x)=|x-a|,不等式f(x)≤3的解集为{x|-1≤x≤5},
∴|x-a|≤3的解集为{x|-1≤x≤5},
∵由|x-a|≤3,解得a-3≤x≤a+3,
∴
|
(Ⅱ)由(Ⅰ)知,f(x)=|x-2|,
∵f(x)+f(x+5)≥m对一切实数x恒成立,
∴|x-2|+|x+3|≥m对一切实数x恒成立.
设y=|x-2|+|x+3|,
由x-2=0,得x=2;由x+3=0,得x=-3.
①当x≥2时,y=x-2+x+3=2x+1≥5;
②当-3≤x<2时,y=2-x+x+3=5;
③当x<-3时,y=2-x-x-3=-2x-1>5.
综上所述,y=|x-2|+|x+3|≥5.
∴若f(x)+f(x+5)≥m对一切实数x恒成立,则m≤5.
故实数m的取值范围是(-∞,5].
点评:A考查与圆有关的比例线段的应用,B考查参数方程的应用,C考查含绝对值不等式的解法.它们都是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.
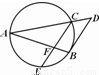
本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分. ,则线段CD的长为 .
,则线段CD的长为 .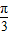 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .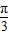 )的直角坐标是 .
)的直角坐标是 .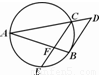
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .