摘要:③综合①②.猜想对任何都成立. --10分
网址:http://m.1010jiajiao.com/timu_id_484962[举报]
 ∴当n=k+1时,不等式成立.
∴当n=k+1时,不等式成立.
根据(1)和(2)可知对任何![]() 都成立.则上述证法( )
都成立.则上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>(08年朝阳区综合练习一)(14分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(Ⅰ)求![]() 的值,猜想
的值,猜想![]() 的表达式,并用数学归纳法证明;
的表达式,并用数学归纳法证明;
(Ⅱ)将数列![]() 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ,
,![]() );(
);(![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ,
,![]() );(
);(![]() ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)设![]() 为数列
为数列 的前
的前![]() 项积,是否存在实数
项积,是否存在实数![]() ,使得不等式
,使得不等式![]() 对一切
对一切![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分13分)
设数列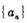 的前n项和为
的前n项和为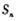 ,对一切
,对一切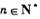 ,点(
,点(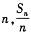 )都在函数
)都在函数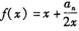 的图象上.
的图象上.
(1) 求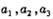 的值,猜想
的值,猜想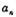 的表达式,并证明你的猜想;
的表达式,并证明你的猜想;
(2) 设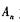 为数列
为数列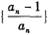 的前项积,是否存在实数、使得不等式
的前项积,是否存在实数、使得不等式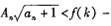
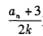 对一切
对一切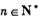 都成立?若存在,求出k的取值范围,若不存在,说明理由.
都成立?若存在,求出k的取值范围,若不存在,说明理由.
查看习题详情和答案>>
 的前
的前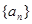 满足
满足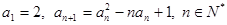 .
.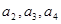 ,并由此猜想
,并由此猜想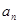 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论;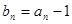 ,不等式
,不等式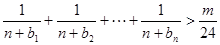 对一切
对一切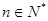 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。