摘要:(2)猜想 --5分证明:①当n=1时.猜想成立. --6分
网址:http://m.1010jiajiao.com/timu_id_484959[举报]
已知Sn是数列{
}的前n项和,
(1)分别计算S2-S1,S4-S2,S8-S4的值;
(2)证明:当n≥1时,S2^-S2n-1≥
,并指出等号成立条件;
(3)利用(2)的结论,找出一个适当的T∈N,使得ST>2010;
(4)是否存在关于正整数n的函数f(n),使得S1+S2+…+Sn-1=f(n)(Sn-1)对于大于1的正整数n都成立?证明你的结论. 查看习题详情和答案>>
| 1 |
| n |
(1)分别计算S2-S1,S4-S2,S8-S4的值;
(2)证明:当n≥1时,S2^-S2n-1≥
| 1 |
| 2 |
(3)利用(2)的结论,找出一个适当的T∈N,使得ST>2010;
(4)是否存在关于正整数n的函数f(n),使得S1+S2+…+Sn-1=f(n)(Sn-1)对于大于1的正整数n都成立?证明你的结论. 查看习题详情和答案>>
已知Sn是数列{
}的前n项和;
(1)分别计算S2-S1,S4-S2,S8-S4的值;
(2)证明:当n≥1时,S2n-S2n-1≥
,并指出等号成立条件;
(3)利用(2)的结论,找出一个适当的T∈N,使得Sr>2008. 查看习题详情和答案>>
| 1 |
| n |
(1)分别计算S2-S1,S4-S2,S8-S4的值;
(2)证明:当n≥1时,S2n-S2n-1≥
| 1 |
| 2 |
(3)利用(2)的结论,找出一个适当的T∈N,使得Sr>2008. 查看习题详情和答案>>
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤ 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明 (
( ).
).
【解析】(1)解:
 的定义域为
的定义域为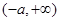

由 ,得
,得
当x变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
因此, 在
在 处取得最小值,故由题意
处取得最小值,故由题意 ,所以
,所以
(2)解:当 时,取
时,取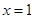 ,有
,有 ,故
,故 时不合题意.当
时不合题意.当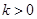 时,令
时,令 ,即
,即

令 ,得
,得
①当 时,
时, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上单调递减.从而对于任意的
上单调递减.从而对于任意的 ,总有
,总有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合题意.
符合题意.
②当 时,
时, ,对于
,对于 ,
, ,故
,故 在
在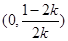 上单调递增.因此当取
上单调递增.因此当取 时,
时, ,即
,即 不成立.
不成立.
故 不合题意.
不合题意.
综上,k的最小值为 .
.
(3)证明:当n=1时,不等式左边= =右边,所以不等式成立.
=右边,所以不等式成立.
当 时,
时,


在(2)中取 ,得
,得
 ,
,
从而

所以有





综上,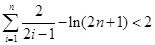 ,
,
查看习题详情和答案>>



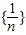 的前n项和;
的前n项和;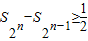 ,并指出等号成立条件;
,并指出等号成立条件;