题目内容
已知Sn是数列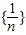 的前n项和;
的前n项和;(1)分别计算S2-S1,S4-S2,S8-S4的值;
(2)证明:当n≥1时,
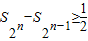 ,并指出等号成立条件;
,并指出等号成立条件;(3)利用(2)的结论,找出一个适当的T∈N,使得Sr>2008.
【答案】分析:(1)较为简单,代入可计算;
(2)由(1)可猜想(2)的结论也是成立的,证明时要适当的放缩每一项(共2n-1项)都缩小为 ,
,
(3)的解答可由(2)的结论想到:新数列S2-S1,S4-S2,S8-S4…中每一项的值都大于等于 ,那么4018项的和为2009,于是对于数列{an}中连同a1就有24019项,即a1+
,那么4018项的和为2009,于是对于数列{an}中连同a1就有24019项,即a1+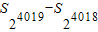 >1+2009=2010.
>1+2009=2010.
解答:解:
(1)S2-S1= ,
,
S4-S2=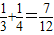 ,
,
S8-S4=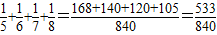 .(2分)
.(2分)
(2)当n≥1时,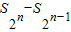 =
=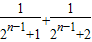 +…+
+…+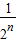 (共2n-1项)
(共2n-1项)
≥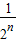 ×2n-1=
×2n-1= ,当且仅当n=1时,等号成立.(4分)
,当且仅当n=1时,等号成立.(4分)
(3)由于S1=1,当n≥1时,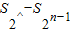 ≥
≥ ,
,
于是,要使得ST>2008,只需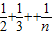 >2007.
>2007.
将 按照第一组21项,第二组22项,,第n组2n项的方式分组(6分)
按照第一组21项,第二组22项,,第n组2n项的方式分组(6分)
由(2)可知,每一组的和不小于 ,且只有n=1时等于
,且只有n=1时等于  ,
,
将这样的分组连续取2×2007组,加上a1,共有24015项,
这24015项之和一定大于1+2007=2008,
故只需T=24015,就能使得ST>2008.
点评:本题考查了数列前n项和的概念,不等式恒成立问题,合理猜想与逻辑推理的概念.对不等式的考查有一定的难度,综合性较强,需要同学有深厚的功底才能胜任本题的解答.
(2)由(1)可猜想(2)的结论也是成立的,证明时要适当的放缩每一项(共2n-1项)都缩小为
 ,
,(3)的解答可由(2)的结论想到:新数列S2-S1,S4-S2,S8-S4…中每一项的值都大于等于
 ,那么4018项的和为2009,于是对于数列{an}中连同a1就有24019项,即a1+
,那么4018项的和为2009,于是对于数列{an}中连同a1就有24019项,即a1+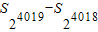 >1+2009=2010.
>1+2009=2010.解答:解:
(1)S2-S1=
 ,
,S4-S2=
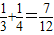 ,
,S8-S4=
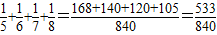 .(2分)
.(2分)(2)当n≥1时,
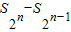 =
=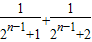 +…+
+…+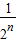 (共2n-1项)
(共2n-1项)≥
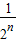 ×2n-1=
×2n-1= ,当且仅当n=1时,等号成立.(4分)
,当且仅当n=1时,等号成立.(4分)(3)由于S1=1,当n≥1时,
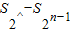 ≥
≥ ,
,于是,要使得ST>2008,只需
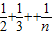 >2007.
>2007.将
 按照第一组21项,第二组22项,,第n组2n项的方式分组(6分)
按照第一组21项,第二组22项,,第n组2n项的方式分组(6分)由(2)可知,每一组的和不小于
 ,且只有n=1时等于
,且只有n=1时等于  ,
,将这样的分组连续取2×2007组,加上a1,共有24015项,
这24015项之和一定大于1+2007=2008,
故只需T=24015,就能使得ST>2008.
点评:本题考查了数列前n项和的概念,不等式恒成立问题,合理猜想与逻辑推理的概念.对不等式的考查有一定的难度,综合性较强,需要同学有深厚的功底才能胜任本题的解答.

练习册系列答案
相关题目
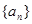 的前n项和,且
的前n项和,且
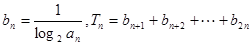 ,是否存在最大的正整数k,使得对于任意的正整数n,有
,是否存在最大的正整数k,使得对于任意的正整数n,有 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.  }的前n项和,则
}的前n项和,则 等于( )
等于( )


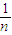 }的前n项和,
}的前n项和,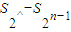 ≥
≥ ,并指出等号成立条件;
,并指出等号成立条件;