摘要：不妨设.则.．
网址：http://m.1010jiajiao.com/timu_id_484876[举报]
函数y=ax3+bx2+cx+d（a≠0）的导函数为y=3ax2+2bx+c，不妨把方程y=3ax2+2bx+c=0称为导方程，其判别式△=4（b2-3ac），若△＞0，设其两根为x1，x2，则当a＜0，△≤0时，三次函数的图象是（ ）
查看习题详情和答案>>
已知函数y=f（x）（x∈D），方程f（x）=x的根x0称为函数f（x）的不动点；若a1∈D，an+1=f（an）（n∈N*），则称{an} 为由函数f（x）导出的数列．
设函数g（x）=
，h（x）=
(c≠0，ad-bc≠0，(d-a)2+4bc＞0)
（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证{
}是等比数列，并求
an；
（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期． 查看习题详情和答案>>
设函数g（x）=
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证{
| an-x1 |
| an-x2 |
| lim |
| n→∞ |
（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期． 查看习题详情和答案>>
已知函数y=f（x）（x∈D），方程f（x）=x的根x0称为函数f（x）的不动点；若a1∈D，an+1=f（an）（n∈N*），则称{an} 为由函数f（x）导出的数列．
设函数g（x）=
，h（x）=
（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证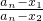
是等比数列，并求
；
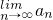（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期．
查看习题详情和答案>>
已知函数y=f（x）（x∈D），方程f（x）=x的根x0称为函数f（x）的不动点；若a1∈D，an+1=f（an）（n∈N*），则称{an} 为由函数f（x）导出的数列．
设函数g（x）=
，h（x）=
(c≠0，ad-bc≠0，(d-a)2+4bc＞0)
（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证{
}是等比数列，并求
an；
（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期．
查看习题详情和答案>>
设函数g（x）=
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证{
| an-x1 |
| an-x2 |
| lim |
| n→∞ |
（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期．
已知函数y=f（x）（x∈D），方程f（x）=x的根x称为函数f（x）的不动点；若a1∈D，an+1=f（an）（n∈N*），则称{an} 为由函数f（x）导出的数列．
设函数g（x）=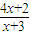
，h（x）=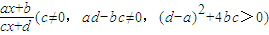
（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证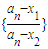
是等比数列，并求
；
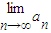（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期．
查看习题详情和答案>>
设函数g（x）=
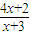，h（x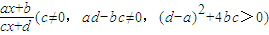）=（1）求函数g（x）的不动点x1，x2；
（2）设a1=3，{an} 是由函数g（x）导出的数列，对（1）中的两个不动点x1，x2（不妨设x1＜x2），数列求证
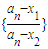是等比数列，并求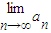；（3）试探究由函数h（x）导出的数列{bn}，（其中b1=p）为周期数列的充要条件．
注：已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+T=bn，则称数列{bn} 为周期数列，T是它的一个周期．
查看习题详情和答案>>