题目内容
函数y=ax3+bx2+cx+d(a≠0)的导函数为y=3ax2+2bx+c,不妨把方程y=3ax2+2bx+c=0称为导方程,其判别式△=4(b2-3ac),若△>0,设其两根为x1,x2,则当a<0,△≤0时,三次函数的图象是( )
分析:利用导方程和对应二次函数的关系,利用二次函数的图象和性质确定函数的单调性.
解答:解:若a<0,则当x→+∞时,y<0,当x→-∞时,y>0,
所以排除C,D.
因为a<0,△≤0,
所以导方程y=3ax2+2bx+c=0对应的二次函数y=3ax2+2bx+c≤0恒成立,
即函数y=ax3+bx2+cx+d(a≠0)单调递减,所以排除A,选B.
故选B.
所以排除C,D.
因为a<0,△≤0,
所以导方程y=3ax2+2bx+c=0对应的二次函数y=3ax2+2bx+c≤0恒成立,
即函数y=ax3+bx2+cx+d(a≠0)单调递减,所以排除A,选B.
故选B.
点评:本题主要考查函数的单调性和导数之间的关系,利用a<0,△≤0,得到二次函数y=3ax2+2bx+c≤0恒成立,是解决本题的关键.

练习册系列答案
相关题目
若y=ax与y=-
在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是( )
| b |
| x |
| A、在(-∞,+∞)上是增函数 |
| B、在(0,+∞)上是增函数 |
| C、在(-∞,+∞)上是减函数 |
| D、在(-∞,0)上是增函数,在(0,+∞)上是减函数 |
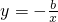 在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是
在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是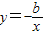 在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是( )
在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是( )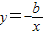 在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是( )
在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是( )