网址:http://m.1010jiajiao.com/timu_id_484854[举报]
(本小题满分12分)已知函数
(I)若函数 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(II)当 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(Ⅲ)求证:解:(1) ,其定义域为
,其定义域为 ,则
,则 令
令 ,
,
则 ,
,
当 时,
时, ;当
;当 时,
时,
 在(0,1)上单调递增,在
在(0,1)上单调递增,在 上单调递减,
上单调递减,
即当 时,函数
时,函数 取得极大值. (3分)
取得极大值. (3分)
 函数
函数 在区间
在区间 上存在极值,
上存在极值,
 ,解得
,解得 (4分)
(4分)
(2)不等式 ,即
,即
令
(6分)
令 ,则
,则 ,
,
 ,即
,即 在
在 上单调递增, (7分)
上单调递增, (7分)
 ,从而
,从而 ,故
,故 在
在 上单调递增, (7分)
上单调递增, (7分)
 (8分)
(8分)
(3)由(2)知,当 时,
时, 恒成立,即
恒成立,即 ,
,
令 ,则
,则 , (9分)
, (9分)

(10分)
以上各式相加得,

即 ,
,
即
 (12分)
(12分)
 。
。
查看习题详情和答案>>
设f (x)=sin 2x+ (sin x-cos x)(sin x+cos x),其中x∈R.
(sin x-cos x)(sin x+cos x),其中x∈R.
(Ⅰ) 该函数的图象可由
 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(Ⅱ)若f (θ)= ,其中
,其中 ,求cos(θ+
,求cos(θ+ )的值;
)的值;
【解析】第一问中,
即 变换分为三步,①把函数
变换分为三步,①把函数 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数 的图象;
的图象;
第二问中因为 ,所以
,所以 ,则
,则 ,又
,又
 ,
, ,从而
,从而
进而得到结论。
(Ⅰ) 解:
即 。…………………………………3分
。…………………………………3分
变换的步骤是:
①把函数 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数 的图象;…………………………………3分
的图象;…………………………………3分
(Ⅱ) 解:因为 ,所以
,所以 ,则
,则 ,又
,又
 ,
, ,从而
,从而 ……2分
……2分
(1)当 时,
时, ;…………2分
;…………2分
(2)当 时;
时;
查看习题详情和答案>>
(1)若(b,c)在直线2x+y=0上,求证:Pz在圆C1:(x-1)2+y2=1上;
(2)给定圆C:(x-m)2+y2=r2(m、r∈R,r>0),则存在唯一的线段s满足:①若Pz在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则Pz在圆C上、写出线段s的表达式,并说明理由;
(3)由(2)知线段s与圆C之间确定了一种对应关系,通过这种对应关系的研究,填写表(表中s1是(1)中圆C1的对应线段).
| 线段s与线段s1的关系 | m、r的取值或表达式 |
| s所在直线平行于s1所在直线 | |
| s所在直线平分线段s1 |
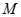 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0, ),(0,
),(0,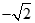 ),又点
),又点
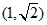 在椭圆
在椭圆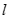 的斜率为
的斜率为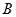 、
、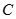 两点,求
两点,求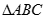 面积的最大值.
面积的最大值.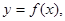 当
当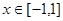 时,
时,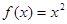 ,则函数
,则函数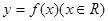 的图象与
的图象与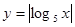 的图象的交点个数为
的图象的交点个数为