题目内容
已知椭圆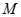 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0, ),(0,
),(0,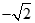 ),又点
),又点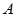
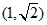 在椭圆
在椭圆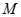 上.
上.
(1)求椭圆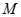 的方程;
的方程;
(2)已知直线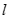 的斜率为
的斜率为 ,若直线
,若直线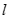 与椭圆
与椭圆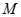 交于
交于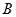 、
、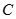 两点,求
两点,求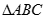 面积的最大值.
面积的最大值.
【答案】
(1)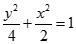 (2)
(2)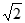
【解析】
试题分析:解: (Ⅰ)由已知抛物线的焦点为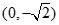 ,故设椭圆方程为
,故设椭圆方程为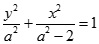 .
.
将点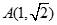 代入方程得
代入方程得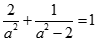 ,整理得
,整理得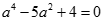 ,
,
解得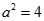 或
或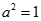 (舍).故所求椭圆方程为
(舍).故所求椭圆方程为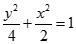 .
.
(Ⅱ)设直线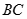 的方程为
的方程为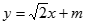 ,设
,设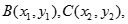
代入椭圆方程并化简得 ,
,
由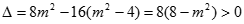 ,可得
,可得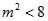 ①.
①.
由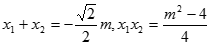 ,
,
故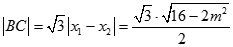 .
.
又点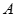 到
到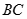 的距离为
的距离为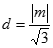 ,
,
故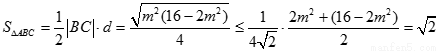 ,
,
当且仅当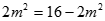 ,即
,即 时取等号(满足①式)
时取等号(满足①式)
所以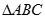 面积的最大值为
面积的最大值为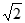 .
.
考点:椭圆的方程
点评:关于曲线的大题,第一问一般是求出曲线的方程,第二问常与直线结合起来,当涉及到交点时,常用到根与系数的关系式: (
( )。
)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆的对称轴为坐标轴,短轴的一个端点和两个焦点的连线构成一个正三角形,且焦点到椭圆上的点的最短距离为
,则椭圆的方程为( )
| 3 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 ,短轴长为4,(1)求椭圆的方程;
,短轴长为4,(1)求椭圆的方程; 两点,求AB的中点坐标及其弦长|AB|。
两点,求AB的中点坐标及其弦长|AB|。