摘要:解:(1)由条件知.可设椭圆方程为
网址:http://m.1010jiajiao.com/timu_id_484815[举报]
已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 <
< 时,求实数
时,求实数 的取值范围.
的取值范围.
【解析】本试题主要考查了椭圆的方程以及直线与椭圆的位置关系的运用。
第一问中,利用
第二问中,利用直线与椭圆联系,可知得到一元二次方程中 ,可得k的范围,然后利用向量的
,可得k的范围,然后利用向量的 <
< 不等式,表示得到t的范围。
不等式,表示得到t的范围。
解:(1)由题意知

查看习题详情和答案>>
(本小题满分14分)
设 椭圆方程为
椭圆方程为 抛物线方程为
抛物线方程为 如图4所示,过点
如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。

查看习题详情和答案>>
(本小题满分14分)
设![]() 椭圆方程为
椭圆方程为![]() 抛物线方程为
抛物线方程为![]() 如图4所示,过点
如图4所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点![]()
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。

 的动直线
的动直线 与抛物线
与抛物线 相交于
相交于 两点.当直线
两点.当直线 时,
时, .
. 的方程;
的方程; 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为 ,求
,求 ,C
,C ,当直线
,当直线 ,即
,即 (1’)
(1’) 得
得 ,
, (3’)
(3’) ,
, (4’)
(4’) G方程为
G方程为 (5’)
(5’) ,BC中点坐标为
,BC中点坐标为 (6’)
(6’) 得
得 由
由 得
得 (8’)
(8’)

 (10’)
(10’) (11’)
(11’)
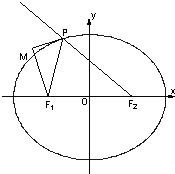 已知如图,椭圆方程为
已知如图,椭圆方程为