摘要:(3)设各项为正的无穷数列满足.证明:.雅安中学高2009届4月月考数学(理)答案1―5CBDAB 6―10ABABD 11―12 DA
网址:http://m.1010jiajiao.com/timu_id_484772[举报]
设各项均为正实数的数列{an}的前n项和为Sn,且满足4Sn=(an+1)2(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}的通项公式为bn=
(t∈N*),若b1,b2,bm(m≥3,m∈N*)成等差数列,求t和m的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列{an}中的三项an1,an2,an3.
查看习题详情和答案>>
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}的通项公式为bn=
| an | an+t |
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列{an}中的三项an1,an2,an3.
设各项均为正实数的数列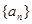 的前
的前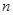 项和为
项和为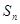 ,且满足
,且满足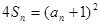 (
(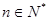 ).
).
(Ⅰ)求数列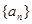 的通项公式;
的通项公式;
(Ⅱ)设数列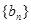 的通项公式为
的通项公式为 (
(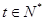 ),若
),若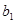 ,
,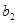 ,
,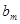 (
(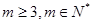 )成等差数列,求
)成等差数列,求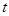 和
和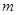 的值;
的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列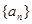 中的三项
中的三项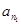 ,
, ,
,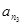 .
.
查看习题详情和答案>>
设各项均为正实数的数列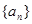 的前
的前 项和为
项和为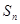 ,且满足
,且满足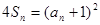 (
(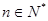 ).
).
(Ⅰ)求数列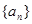 的通项公式;
的通项公式;
(Ⅱ)设数列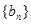 的通项公式为
的通项公式为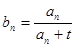 (
(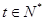 ),若
),若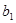 ,
,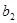 ,
,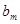 (
(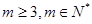 )成等差数列,求
)成等差数列,求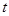 和
和 的值;
的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列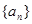 中的三项
中的三项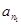 ,
,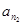 ,
,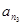 .
.
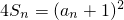 (n∈N*).
(n∈N*).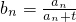 (t∈N*),若b1,b2,bm(m≥3,m∈N*)成等差数列,求t和m的值;
(t∈N*),若b1,b2,bm(m≥3,m∈N*)成等差数列,求t和m的值;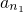 ,
,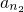 ,
,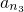 .
.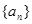 的前
的前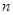 项和为
项和为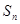 ,且满足
,且满足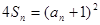 (
(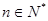 ).
).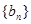 的通项公式为
的通项公式为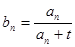 (
(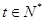 ),若
),若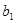 ,
,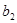 ,
,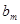 (
(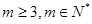 )成等差数列,求
)成等差数列,求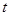 和
和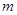 的值;
的值;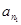 ,
,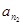 ,
,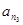 .
.