题目内容
设各项均为正实数的数列{an}的前n项和为Sn,且满足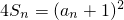 (n∈N*).
(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}的通项公式为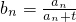 (t∈N*),若b1,b2,bm(m≥3,m∈N*)成等差数列,求t和m的值;
(t∈N*),若b1,b2,bm(m≥3,m∈N*)成等差数列,求t和m的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列{an}中的三项 ,
, ,
,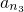 .
.
解:(Ⅰ)由题意,4Sn=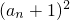 ①,
①,
当n≥2时,有4Sn-1=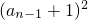 ②,
②,
②-①,得(an+an-1)(an-an-1-2)=0,
∵{an}各项为正,
∴an+an-1>0,
从而an-an-1=2,故{an}成公差2的等差数列.
又n=1时,4a1=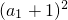 ,解得a1=1.故an=2n-1. …(4分)
,解得a1=1.故an=2n-1. …(4分)
(Ⅱ)bn=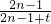 ,要使b1,b2,bm成等差数列,须2b2=b1+bm,
,要使b1,b2,bm成等差数列,须2b2=b1+bm,
即2×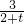 =
= +
+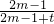 ,整理得m=3+
,整理得m=3+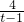 ,
,
因为m,t为正整数,t只能取2,3,5.
故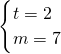 ,
, ,
,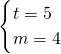 . …(10分)
. …(10分)
(Ⅲ)作如下构造: =(2k+3)2,
=(2k+3)2, =(2k+3)(2k+5),
=(2k+3)(2k+5),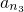 =(2k+5)2,其中k∈N*,它们依次为数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,
=(2k+5)2,其中k∈N*,它们依次为数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,
显然它们成等比数列,且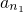 +
+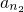 >
>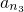 ,所以它们能组成三角形.
,所以它们能组成三角形.
由k∈N*的任意性,知这样的三角形有无穷多个.
下面用反证法证明其中任意两个三角形△A1B1C1与△A2B2C2不相似.
若△A1B1C1∽△A2B2C2,且k1≠k2,则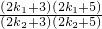 =
=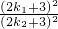 ,整理得
,整理得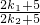 =
=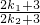 ,所以k1=k2,这与k1≠k2矛盾,因此,任意两个三角形不相似.故原命题正确. …(16分)
,所以k1=k2,这与k1≠k2矛盾,因此,任意两个三角形不相似.故原命题正确. …(16分)
分析:(Ⅰ)由4Sn=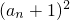 ①,类推,当n≥2时,有4Sn-1=
①,类推,当n≥2时,有4Sn-1=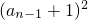 ②,作差后依题意得到an-an-1=2,再求得a1=1即可求得数列{an}的通项公式;
②,作差后依题意得到an-an-1=2,再求得a1=1即可求得数列{an}的通项公式;
(Ⅱ)依题意,要使b1,b2,bm成等差数列,须2b2=b1+bm,整理得m=3+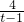 ,由m,t为正整数,可求得t,m的值;
,由m,t为正整数,可求得t,m的值;
(Ⅲ)构造: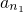 =(2k+3)2,
=(2k+3)2,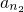 =(2k+3)(2k+5),
=(2k+3)(2k+5),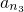 =(2k+5)2,其中k∈N*,使之成数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,它们成等比数列且能组成三角形,可利用反证法证得任意两个三角形△A1B1C1与△A2B2C2不相似.
=(2k+5)2,其中k∈N*,使之成数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,它们成等比数列且能组成三角形,可利用反证法证得任意两个三角形△A1B1C1与△A2B2C2不相似.
点评:本题考查数列与三角函数的综合,考查等差数列的推证与通项的求法,突出考查构造数列与推理论证的能力,属于难题.
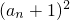 ①,
①,当n≥2时,有4Sn-1=
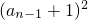 ②,
②,②-①,得(an+an-1)(an-an-1-2)=0,
∵{an}各项为正,
∴an+an-1>0,
从而an-an-1=2,故{an}成公差2的等差数列.
又n=1时,4a1=
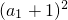 ,解得a1=1.故an=2n-1. …(4分)
,解得a1=1.故an=2n-1. …(4分)(Ⅱ)bn=
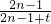 ,要使b1,b2,bm成等差数列,须2b2=b1+bm,
,要使b1,b2,bm成等差数列,须2b2=b1+bm,即2×
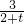 =
= +
+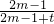 ,整理得m=3+
,整理得m=3+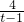 ,
,因为m,t为正整数,t只能取2,3,5.
故
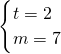 ,
, ,
,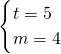 . …(10分)
. …(10分)(Ⅲ)作如下构造:
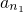 =(2k+3)2,
=(2k+3)2,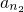 =(2k+3)(2k+5),
=(2k+3)(2k+5),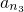 =(2k+5)2,其中k∈N*,它们依次为数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,
=(2k+5)2,其中k∈N*,它们依次为数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,显然它们成等比数列,且
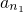 +
+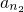 >
>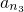 ,所以它们能组成三角形.
,所以它们能组成三角形.由k∈N*的任意性,知这样的三角形有无穷多个.
下面用反证法证明其中任意两个三角形△A1B1C1与△A2B2C2不相似.
若△A1B1C1∽△A2B2C2,且k1≠k2,则
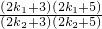 =
=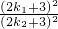 ,整理得
,整理得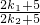 =
=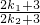 ,所以k1=k2,这与k1≠k2矛盾,因此,任意两个三角形不相似.故原命题正确. …(16分)
,所以k1=k2,这与k1≠k2矛盾,因此,任意两个三角形不相似.故原命题正确. …(16分)分析:(Ⅰ)由4Sn=
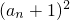 ①,类推,当n≥2时,有4Sn-1=
①,类推,当n≥2时,有4Sn-1=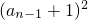 ②,作差后依题意得到an-an-1=2,再求得a1=1即可求得数列{an}的通项公式;
②,作差后依题意得到an-an-1=2,再求得a1=1即可求得数列{an}的通项公式;(Ⅱ)依题意,要使b1,b2,bm成等差数列,须2b2=b1+bm,整理得m=3+
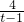 ,由m,t为正整数,可求得t,m的值;
,由m,t为正整数,可求得t,m的值;(Ⅲ)构造:
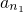 =(2k+3)2,
=(2k+3)2,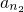 =(2k+3)(2k+5),
=(2k+3)(2k+5),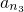 =(2k+5)2,其中k∈N*,使之成数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,它们成等比数列且能组成三角形,可利用反证法证得任意两个三角形△A1B1C1与△A2B2C2不相似.
=(2k+5)2,其中k∈N*,使之成数列{an}中第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13,它们成等比数列且能组成三角形,可利用反证法证得任意两个三角形△A1B1C1与△A2B2C2不相似.点评:本题考查数列与三角函数的综合,考查等差数列的推证与通项的求法,突出考查构造数列与推理论证的能力,属于难题.

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,已知
,已知 ,数
,数 是公差为
是公差为 的等差数列。
的等差数列。 表示);
表示); 为实数,对满足
为实数,对满足 的任意正整数
的任意正整数 ,不等式
,不等式 都成立。求证:
都成立。求证: 。
。