题目内容
设各项均为正实数的数列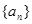 的前
的前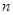 项和为
项和为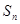 ,且满足
,且满足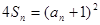 (
(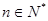 ).
).
(Ⅰ)求数列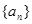 的通项公式;
的通项公式;
(Ⅱ)设数列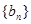 的通项公式为
的通项公式为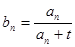 (
(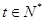 ),若
),若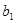 ,
,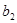 ,
,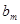 (
(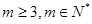 )成等差数列,求
)成等差数列,求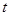 和
和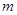 的值;
的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列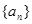 中的三项
中的三项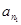 ,
,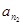 ,
,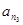 .
.
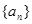 的前
的前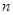 项和为
项和为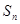 ,且满足
,且满足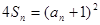 (
(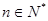 ).
).(Ⅰ)求数列
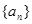 的通项公式;
的通项公式;(Ⅱ)设数列
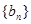 的通项公式为
的通项公式为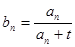 (
(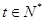 ),若
),若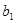 ,
,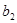 ,
,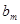 (
(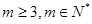 )成等差数列,求
)成等差数列,求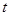 和
和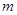 的值;
的值;(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列
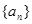 中的三项
中的三项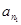 ,
,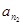 ,
,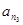 .
.(Ⅰ)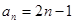 ;(Ⅱ)
;(Ⅱ)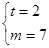 ,
,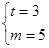 ,
,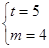 .
.
(Ⅲ)作如下构造: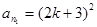 ,
,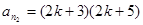 ,
,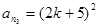 ,其中
,其中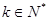 ,它们依次为数列
,它们依次为数列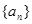 中第
中第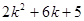 项,第
项,第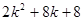 项,第
项,第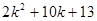 ,显然它们成等比数列,且
,显然它们成等比数列,且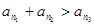 ,所以它们能组成三角形.
,所以它们能组成三角形.
由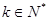 的任意性,知这样的三角形有无穷多个.
的任意性,知这样的三角形有无穷多个.
用反证法证明其中任意两个 和
和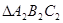 不相似
不相似
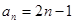 ;(Ⅱ)
;(Ⅱ)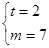 ,
,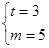 ,
,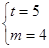 .
. (Ⅲ)作如下构造:
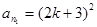 ,
,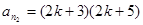 ,
,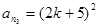 ,其中
,其中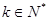 ,它们依次为数列
,它们依次为数列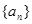 中第
中第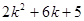 项,第
项,第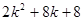 项,第
项,第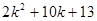 ,显然它们成等比数列,且
,显然它们成等比数列,且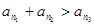 ,所以它们能组成三角形.
,所以它们能组成三角形.由
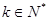 的任意性,知这样的三角形有无穷多个.
的任意性,知这样的三角形有无穷多个. 用反证法证明其中任意两个
 和
和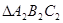 不相似
不相似 试题分析:(Ⅰ)由题意,
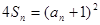 ①,当
①,当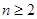 时,有
时,有 ②,
②,②-①,得
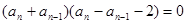 ,
,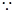
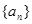 各项为正,
各项为正,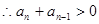 ,
,从而
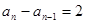 ,故
,故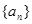 成公差2的等差数列.又
成公差2的等差数列.又 时,
时,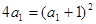 ,解得
,解得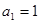 .故
.故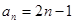 . 4分
. 4分(Ⅱ)
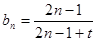 ,要使
,要使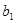 ,
,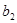 ,
,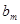 成等差数列,须
成等差数列,须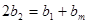 ,
,即
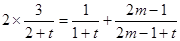 ,整理得
,整理得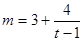 ,因为
,因为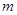 ,
,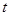 为正整数,
为正整数,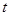 只能取2,3,5.故
只能取2,3,5.故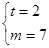 ,
,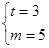 ,
,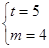 . 10分
. 10分(Ⅲ)作如下构造:
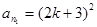 ,
,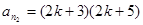 ,
,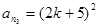 ,其中
,其中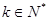 ,它们依次为数列
,它们依次为数列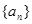 中第
中第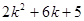 项,第
项,第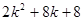 项,第
项,第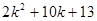 ,显然它们成等比数列,且
,显然它们成等比数列,且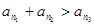 ,所以它们能组成三角形.
,所以它们能组成三角形.由
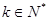 的任意性,知这样的三角形有无穷多个.
的任意性,知这样的三角形有无穷多个. 下面用反证法证明其中任意两个
 和
和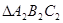 不相似:若
不相似:若 ∽
∽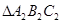 ,且
,且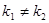 ,则
,则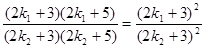 ,整理得
,整理得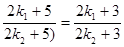 ,所以
,所以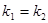 ,这与
,这与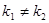 矛盾,因此,任意两个三角形不相似.故原命题正确. 16分
矛盾,因此,任意两个三角形不相似.故原命题正确. 16分点评:基础题,首先利用
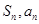 的关系,确定得到
的关系,确定得到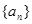 的通项公式,进一步研究
的通项公式,进一步研究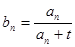 中项的关系。为证明
中项的关系。为证明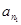 ,
,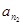 ,
,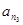 能构成三角形,在明确表达式的基础上,应用了反证法。
能构成三角形,在明确表达式的基础上,应用了反证法。
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 }满足
}满足 =1,
=1, =
= ,(1)计算
,(1)计算 ,
, ,
, 的值;(2)归纳推测
的值;(2)归纳推测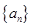 的通项
的通项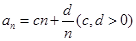 ,第2项是最小项,则
,第2项是最小项,则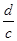 的取值范围是 .
的取值范围是 .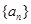 是等差数列,首项
是等差数列,首项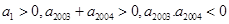 ,则使前n项和
,则使前n项和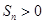 成立的最大自然数n是( )
成立的最大自然数n是( )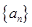 的公比
的公比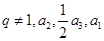 成等差数列,则
成等差数列,则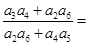 ( )
( )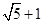
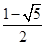

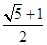
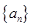 的前
的前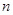 项和为
项和为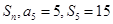 ,则数列
,则数列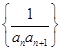 的前100项和为( )
的前100项和为( )



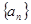 的前
的前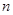 项和为
项和为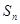
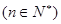 ,设
,设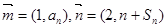 ,且
,且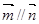 .
.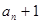 }是等比数列;
}是等比数列;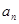 与
与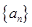 的前
的前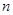 项和为
项和为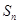 ,若
,若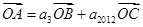 ,且
,且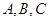 三点共线(该直线不过点
三点共线(该直线不过点 ),则
),则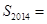 _____________.
_____________.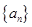 的相邻两项
的相邻两项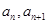 是关于
是关于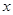 的方程
的方程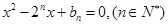 的两根,且
的两根,且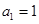 .
.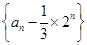 是等比数列;
是等比数列;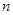 项和
项和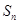 ;
;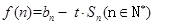 若
若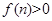 对任意的
对任意的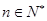 都成立,求
都成立,求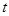 的取值范围。
的取值范围。