摘要:又由的中点E面点到面BDC1的距离=点C到面BDC1的距离.
网址:http://m.1010jiajiao.com/timu_id_481210[举报]
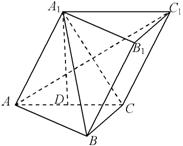
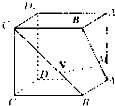 正方体ABCD-A1B1C1D1 中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:
正方体ABCD-A1B1C1D1 中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;
②MN∥平面A1B1C1D1;
③MN与A1C1异面;
④点B1到面BDC1的距离为
| ||
| 3 |
①②③④
①②③④
.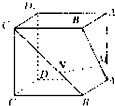 正方体ABCD-A1B1C1D1 中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:
正方体ABCD-A1B1C1D1 中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;
②MN∥平面A1B1C1D1;
③MN与A1C1异面;
④点B1到面BDC1的距离为
| ||
| 3 |
⑤若点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为等边三角形.
其中有可能成立的结论为 ( )
查看习题详情和答案>>
如图,在棱长均为2的正四棱锥 中,点E为PC的中点,则下列命题正确的是( )(正四棱锥即底面为正方形,四条侧棱长相等,顶点在底面上的射影为底面的中心的四棱锥)
中,点E为PC的中点,则下列命题正确的是( )(正四棱锥即底面为正方形,四条侧棱长相等,顶点在底面上的射影为底面的中心的四棱锥)

A. ,且直线BE到面PAD的距离为
,且直线BE到面PAD的距离为
B. ,且直线BE到面PAD的距离为
,且直线BE到面PAD的距离为
C. ,且直线BE与面PAD所成的角大于
,且直线BE与面PAD所成的角大于
D. ,且直线BE与面PAD所成的角小于
,且直线BE与面PAD所成的角小于
查看习题详情和答案>>
 ;⑤若点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为等边三角形.其中有可能成立的结论为 .
;⑤若点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为等边三角形.其中有可能成立的结论为 .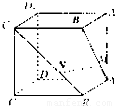
 (Ⅰ)求证:
(Ⅰ)求证: