网址:http://m.1010jiajiao.com/timu_id_481021[举报]
在△ABC中, 为三个内角
为三个内角 为三条边,
为三条边, 且
且
(I)判断△ABC的形状;
(II)若 ,求
,求 的取值范围.
的取值范围.
【解析】本题主要考查正余弦定理及向量运算
第一问利用正弦定理可知,边化为角得到

所以得到B=2C,然后利用内角和定理得到三角形的形状。
第二问中,

得到。
(1)解:由 及正弦定理有:
及正弦定理有:
∴B=2C,或B+2C ,若B=2C,且
,若B=2C,且 ,∴
,∴ ,
, ;∴B+2C
;∴B+2C ,则A=C,∴
,则A=C,∴ 是等腰三角形。
是等腰三角形。
(2)

查看习题详情和答案>>
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积。
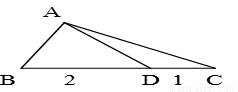
【解析】本试题主要考查了余弦定理的运用。利用由题意得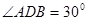 ,
,

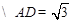 ,
,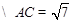 并且
并且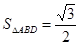 有
有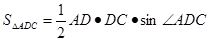 得到结论。
得到结论。
解:(Ⅰ)由题意得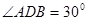 ,
,
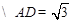 ………1分
………1分 …………1分
…………1分
(Ⅱ)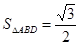 ………………1分
………………1分
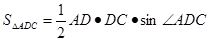
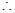
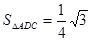

查看习题详情和答案>>
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
查看习题详情和答案>>
 (2)在任意△DEF中,
(2)在任意△DEF中, 某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°,在距C处31公里的公路上的B处有一个人正沿着公路向城A走去,走20公里后到达D处,测得CD=21公里,求这时此人距城A多少公里?某同学甲已经由余弦定理求得cos∠CDB=-
某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°,在距C处31公里的公路上的B处有一个人正沿着公路向城A走去,走20公里后到达D处,测得CD=21公里,求这时此人距城A多少公里?某同学甲已经由余弦定理求得cos∠CDB=-