摘要:(2) 由三角函数的定义可知 --8分
网址:http://m.1010jiajiao.com/timu_id_478661[举报]
如表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是
=-0.7x+a,则a等于( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| ? |
| y |
| A、5.1 | B、5.2 |
| C、5.25 | D、5.4 |
(2013•济南一模)为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若干户家庭的年收入x(单位:万元)和年教育支出y(单位:万元),调查显示年收入x与年教育支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:y=0.15x+0.2.由回归直线方程可知,家庭年收入每增加1万元,年教育支出平均增加
查看习题详情和答案>>
0.15
0.15
万元.
(1)已知抛物线y2=2px(p>0),过焦点F的动直线l交抛物线于A,B两点,为坐标原点,求证:
•
为定值;
(2)由(1)可知:过抛物线的焦点F的动直线l交抛物线于A,B两点,存在定点P,使得
•
为定值.请写出关于椭圆的类似结论,并给出证明.
查看习题详情和答案>>
| OA |
| OB |
(2)由(1)可知:过抛物线的焦点F的动直线l交抛物线于A,B两点,存在定点P,使得
| PA |
| PB |
某市4997名学生参加高中数学会考,得分均在60分以上,现从中随机抽取一个容量为500的样本,制成如图所示的频率分布直方图(图a).
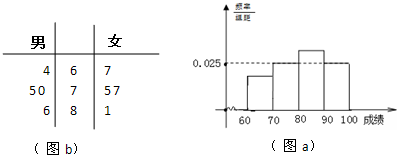
(1)任抽取该市一位学生,求其得分在区间[90,100]的概率(用频率代替概率);
(2)由频率分布直方图可知本次会考的数学平均分为81分.请估计该市得分在区间[60,70]的人数;
(3)如图b所示茎叶图是某班男女各4名学生的得分情况,现用简单随机抽样的方法,从这8名学生中,抽取男女生各一人,求女生得分不低于男生得分的概率. 查看习题详情和答案>>

(1)任抽取该市一位学生,求其得分在区间[90,100]的概率(用频率代替概率);
(2)由频率分布直方图可知本次会考的数学平均分为81分.请估计该市得分在区间[60,70]的人数;
(3)如图b所示茎叶图是某班男女各4名学生的得分情况,现用简单随机抽样的方法,从这8名学生中,抽取男女生各一人,求女生得分不低于男生得分的概率. 查看习题详情和答案>>
下表是1~4月份用水量(单位:百吨)的一组数据:
|
月份x |
1 |
2 |
3 |
4 |
|
用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量y与x之间有较好的线性相关关系,其线性回归直线方程是 ,则a等于
(
)
,则a等于
(
)
A.10.5 B.5.15 C.5.2 D.5.25
查看习题详情和答案>>