题目内容
(1)已知抛物线y2=2px(p>0),过焦点F的动直线l交抛物线于A,B两点,为坐标原点,求证:| OA |
| OB |
(2)由(1)可知:过抛物线的焦点F的动直线l交抛物线于A,B两点,存在定点P,使得
| PA |
| PB |
分析:(1)先讨论出当直线l垂直于x轴时,
•
的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入
•
计算即可得到结论.
(2)先写出类似结论,再根据第一问求
•
的方法即可得到结论.(注意要分直线斜率存在和不存在两种情况讨论).
| OA |
| OB |
| OA |
| OB |
(2)先写出类似结论,再根据第一问求
| OA |
| OB |
解答:解:(1)若直线l垂直于x轴,则A(
,p),B(
,-p).
•
=(
)2-p2=-
p2.…(2分)
若直线l不垂直于轴,设其方程为y=k(x-
),A(x1,y1)B(x2,y2).
由
?k2x2-p(2+k2)x+
k2=0x1+x2=
p,x1•x2=
.…(4分)
∴
•
=x1x2+y1y2=x1x2+k2(x1-
)(x2-
)=(1+k2)x1x2-
k2(x1+x2)+
=(1+k2)
-
k2•
+
=-
p2.
综上,
•
=-
p2为定值.…(6分)
(2)关于椭圆有类似的结论:
过椭圆
+
=1(a>0,b>0)的一个焦点F的动直线l交椭圆于A、B两点,存在定点P,使
•
为定值.
证明:不妨设直线l过椭圆
+
=1的右焦点F(c,0)(其中c=
)
若直线l不垂直于轴,则设其方程为:y=k(x-c),A(x1,y1)B(x2,y2).
由
?(a2k2+b2)x2-2a2ck2x+(a2c2k2-a2b2)=0得:
所以x1+x2=
,x1•x2=
.…(9分)
由对称性可知,设点P在x轴上,其坐标为(m,0).
所以
•
=(x1-m)(x2-m)+y1y2
=(1+k2)x1x2-(m+ck2)(x1+x2)+m2+c2k2
=(1+k2)
-(m+ck2)
+m2+c2k2
=
要使
•
为定值,
只要a4-a2b2-b4+a2m2-2a2cm=a2(m2-a2),
即m=
=
=
此时
•
=m2-a2=
=
…(12分)
若直线l垂直于x轴,则其方程为x=c,A(c,
),B(c,-
).
取点P(
,0)
有
•
=[
-c]2-
=
.…(13分)
综上,过焦点F(c,0)的任意直线l交椭圆于A、B两点,存在定点P(
,0)
使
•
=
.为定值.…(14分)
| p |
| 2 |
| p |
| 2 |
| OA |
| OB |
| p |
| 2 |
| 3 |
| 4 |
若直线l不垂直于轴,设其方程为y=k(x-
| p |
| 2 |
由
|
| p2 |
| 4 |
| (2+k2) |
| k2 |
| p2 |
| 4 |
∴
| OA |
| OB |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p2k2 |
| 4 |
| p2 |
| 4 |
| p |
| 2 |
| (2+k2)p |
| k2 |
| p2k2 |
| 4 |
| 3 |
| 4 |
综上,
| OA |
| OB |
| 3 |
| 4 |
(2)关于椭圆有类似的结论:
过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
证明:不妨设直线l过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
若直线l不垂直于轴,则设其方程为:y=k(x-c),A(x1,y1)B(x2,y2).
由
|
所以x1+x2=
| 2a2ck2 |
| a2k2+b2 |
| a2c2k2-a2b2 |
| a2k2-b2 |
由对称性可知,设点P在x轴上,其坐标为(m,0).
所以
| PA |
| PB |
=(1+k2)x1x2-(m+ck2)(x1+x2)+m2+c2k2
=(1+k2)
| a2c2k2-a2b2 |
| a2k2-b2 |
| 2a2ck2 |
| a2k2+b2 |
=
| (a4-a2b2-b4+a2m2-2a2cm)k2+(m2-a2)b2 |
| a2k2+b2 |
要使
| PA |
| PB |
只要a4-a2b2-b4+a2m2-2a2cm=a2(m2-a2),
即m=
| 2a4-a2b2-b4 |
| 2a2c |
| (2a2+b2)c |
| 2a2 |
| (3-e2)c |
| 2 |
此时
| PA |
| PB |
| (2a2+b2)2c2-4a6 |
| 4a4 |
| b4(c2-4a2) |
| 4a4 |
若直线l垂直于x轴,则其方程为x=c,A(c,
| b2 |
| a |
| b2 |
| a |
取点P(
| (2a2+b2)c |
| 2a2 |
有
| PA |
| PB |
| (2a2+b2)c |
| 2a2 |
| b4 |
| a2 |
| b4(c2-4a2) |
| 4a4 |
综上,过焦点F(c,0)的任意直线l交椭圆于A、B两点,存在定点P(
| (2a2+b2)c |
| 2a2 |
使
| PA |
| PB |
| b4(c2-4a2) |
| 4a4 |
点评:本题主要考查抛物线的基本性质以及直线与圆锥曲线的综合问题.在解决直线与圆锥曲线综合问题时,常把直线方程与圆锥曲线方程联立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
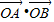 为定值;
为定值;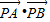 为定值.请写出关于椭圆的类似结论,并给出证明.
为定值.请写出关于椭圆的类似结论,并给出证明.