题目内容
(2013•济南一模)为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若干户家庭的年收入x(单位:万元)和年教育支出y(单位:万元),调查显示年收入x与年教育支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:y=0.15x+0.2.由回归直线方程可知,家庭年收入每增加1万元,年教育支出平均增加
0.15
0.15
万元.分析:写出当自变量增加1时的预报值,用这个预报值去减去自变量x对应的值,得到家庭年收入每增加 1万元,年教育支出平均增加的数字,得到结果.
解答:解:∵对x的回归直线方程y=0.15x+0.2.
∴y1=0.15(x+1)+0.2,
∴y1-y=0.15(x+1)+0.2-0.15x-0.2=0.15,
故答案为:0.15.
∴y1=0.15(x+1)+0.2,
∴y1-y=0.15(x+1)+0.2-0.15x-0.2=0.15,
故答案为:0.15.
点评:本题考查线性回归方程,考查线性回归方程的应用,用来预报当自变量取某一个数值时对应的y的值,注意本题所说的是平均增,注意叙述正确.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
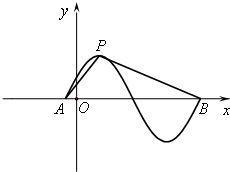 (2013•济南一模)函数y=sin(
(2013•济南一模)函数y=sin(