摘要：∵ 正方形ABCD边长为2 ∴ BG⊥AC.∵ BF⊥平面ACE 由三垂线定理逆定理得FG⊥AC∴ ∠BGF是二面角B―AC―E的平面角由(1)AE⊥平面BCE ∴ AE⊥EB
网址：http://m.1010jiajiao.com/timu_id_476505[举报]
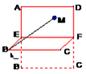
正方形ABCD边长为2，E，F分别是AB和CD的中点，将正方形沿EF折成直二面角（如图），M为矩形AEFD内一点，如果∠MBE=∠MBC，MB和平面BCF所成角的正切值为| 1 |
| 2 |
如图：设一正方形ABCD边长为2分米，切去阴影部分所示的四个全等的等腰三角形，剩余为一个正方形和四个全等的等腰三角形，沿虚线折起，使A、B、C、D四点重合，记为A点．恰好能做成一个正四棱锥（粘贴损耗不计），图中AH⊥PQ，O为正四棱锥底面中心．
（Ⅰ）若正四棱锥的棱长都相等，求这个正四棱锥的体积V；
（Ⅱ）设等腰三角形APQ的底角为x，试把正四棱锥的侧面积S表示为x的函数，并求S的范围．
查看习题详情和答案>>
（Ⅰ）若正四棱锥的棱长都相等，求这个正四棱锥的体积V；
（Ⅱ）设等腰三角形APQ的底角为x，试把正四棱锥的侧面积S表示为x的函数，并求S的范围．
，那么点M到直线EF的距离为( )
B. 1 C. 
D. 
