摘要：又∵BD1平面ABC1D1. ∴B1C⊥BD1. ------8分而EF//BD1.∴EF⊥B1C.------9分
网址：http://m.1010jiajiao.com/timu_id_476399[举报]
正方体ABCD—A1B1C1D1的棱长为1，E、F、G分别为棱AA1、CC1、A1B1的中点，则下列几个命题：
①在空间中与三条直线A1D1，EF，CD都相交的直线有无数条;
②点G到平面ABC1D1的距离为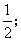
③直线AA1与平面ABC1D1所成的角等于45°；
④空间四边形ABCD1在正方体六个面内形成六个射影，其面积的最小值是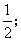
⑤直线A1C1与直线AG所成角的余弦值为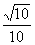
;
⑥若一直线PQ既垂直于A1D,又垂直于AC,则直线PQ与BD1是垂直不相交的关系．
其中真命题是 ．（写出所有真命题的序号）
查看习题详情和答案>>
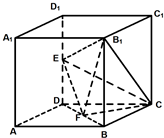如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为DD1、DB的中点．（1）求证：EF∥平面ABC1D1；
（2）求证：EF⊥B1C；
（3）求三棱锥VB1-EFC的体积． 查看习题详情和答案>>
如图，已知平行六面体ABCD-A1B1C1D1．
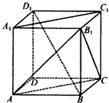如图，在正方体ABCD-A1B1C1D1中，下列结论错误的是（ ）
如图，已知平行六面体ABCD-A1B1C1D1（底面是平行四边形的四棱柱）