摘要:解:(1)关系式为 y=5x.函数如图x,解得x=5.所以.共购进草莓为10+5=15千克共捐款为70-15×3=25(元)
网址:http://m.1010jiajiao.com/timu_id_474848[举报]
问题背景
若矩形的周长为1,则可求出该矩形面积的最大值.我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:  ,利用函数的图象或通过配方均可求得该函数的最大值.
,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为: ,问题就转化为研究该函数的最大(小)值了.
,问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数 的最大(小)值.
的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数 的图象:
的图象:
|
x |
··· |
|
|
|
1 |
2 |
3 |
4 |
··· |
|
y |
|
|
|
|
|
|
|
|
|

(2)观察猜想:观察该函数的图象,猜想当x= 时,函数 有最 值(填
有最 值(填
“大”或“小”),是 .
(3)推理论证:问题背景中提到,通过配方可求二次函数 的最大值,请你尝试通过配方求函数
的最大值,请你尝试通过配方求函数 的最大(小)值,以证明你的猜想. 〔提示:当
的最大(小)值,以证明你的猜想. 〔提示:当 时,
时, 〕
〕
查看习题详情和答案>>
问题背景
若矩形的周长为1,则可求出该矩形面积的最大值.我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:  ,利用函数的图象或通过配方均可求得该函数的最大值.
,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为: ,问题就转化为研究该函数的最大(小)值了.
,问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数 的最大(小)值.
的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数 的图象:
的图象:
| x | ··· |  |  |  | 1 | 2 | 3 | 4 | ··· |
| y | | | | | | | | | |

(2)观察猜想:观察该函数的图象,猜想当x= 时,函数
 有最 值(填
有最 值(填“大”或“小”),是 .
(3)推理论证:问题背景中提到,通过配方可求二次函数
 的最大值,请你尝试通过配方求函数
的最大值,请你尝试通过配方求函数 的最大(小)值,以证明你的猜想. 〔提示:当
的最大(小)值,以证明你的猜想. 〔提示:当 时,
时, 〕
查看习题详情和答案>>
〕
查看习题详情和答案>>



 s2+
s2+ s+
s+ .如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为
.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为 米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是 .
米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是 .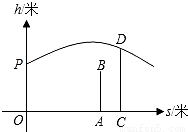
 s2+
s2+ s+
s+ .如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为
.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为 米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是 .
米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是 .