摘要：解之.得
网址：http://m.1010jiajiao.com/timu_id_474609[举报]
14、解方程|x-1|+|x+2|=5．由绝对值的几何意义知，该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值．在数轴上，1和-2的距离为3，满足方程的x对应点在1的右边或-2的左边，若x对应点在1的右边，由图可以看出x=2；同理，若x对应点在-2的左边，可得x=-3，故原方程的解是x=2或x=-3．
参考阅读材料，解答下列问题：
（1）方程|x+3|=4的解为
（2）解不等式|x-3|+|x+4|≥9；
（3）若|x-3|+|x+4|≤a对任意的x都成立，求a的取值范围．
查看习题详情和答案>>
参考阅读材料，解答下列问题：
（1）方程|x+3|=4的解为
1和-7
．（2）解不等式|x-3|+|x+4|≥9；
（3）若|x-3|+|x+4|≤a对任意的x都成立，求a的取值范围．
解决问题：（1）甲、乙同时各掷一枚骰子一次．
（2）求出两个朝上数字的积．
（3）若得到的积为偶数则甲得1分，否则乙得1分．
（4）这个游戏对甲、乙双方公平吗？为什么？
（5）若不公平，你们能修改规则，使之公平吗？你们能想出多少种方法． 查看习题详情和答案>>
（2）求出两个朝上数字的积．
（3）若得到的积为偶数则甲得1分，否则乙得1分．
（4）这个游戏对甲、乙双方公平吗？为什么？
（5）若不公平，你们能修改规则，使之公平吗？你们能想出多少种方法． 查看习题详情和答案>>
解下列方程，将得到的解填入下面的表格中，观察表格中两个解的和与积，它们和原来的方程的系数有什么联系？
（1）x2-2x=0（2）x2+3x-4=0（3）x2-5x+6=0
请同学们仔细观察方程的解，你会发现方程的解与方程中未知数的系数和常数项之间有一定的关系．
一般的，对于关于x的方程x2+px+q=0（p，q为常数，p2-4q≥0）的两根为x1、x2
则x1+x2=
（2）运用以上发现，解决下面的问题：
①已知一元二次方程x2-2x-7=0的两个根为x1，x2，则x1+x2的值为
A．-2 B．2 C．-7 D．7
②已知x1，x2是方程x2-x-3=0的两根，利用上述结论，不解方程，求x12+x22的值．
查看习题详情和答案>>
（1）x2-2x=0（2）x2+3x-4=0（3）x2-5x+6=0
| 方 程 | x1 | x2 | x1+x2 | x1．x2 |
| （1） | 0 0 |
2 2 |
2 2 |
0 0 |
| （2） | -4 -4 |
1 1 |
-3 -3 |
-4 -4 |
| （3） | 2 2 |
3 3 |
5 5 |
6 6 |
一般的，对于关于x的方程x2+px+q=0（p，q为常数，p2-4q≥0）的两根为x1、x2
则x1+x2=
-p
-p
，x1．x2=q
q
．（2）运用以上发现，解决下面的问题：
①已知一元二次方程x2-2x-7=0的两个根为x1，x2，则x1+x2的值为
B
B
A．-2 B．2 C．-7 D．7
②已知x1，x2是方程x2-x-3=0的两根，利用上述结论，不解方程，求x12+x22的值．
解决下面问题：
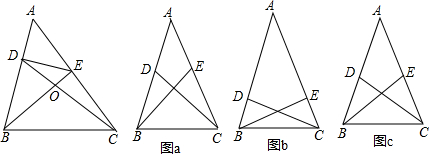
如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且∠DCB=∠EBC=
∠A，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．
小新同学是这样思考的：
在平时的学习中，有这样的经验：假如△ABC是等腰三角形，那么在给定一组对应条件，如图a，BE，CD分别是两底角的平分线（或者如图b，BE，CD分别是两条腰的高线，或者如图c，BE，CD分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角．这个问题也许可以通过添加辅助线构造轴对称图形来解决．请参考小新同学的思路，解决上面这个问题．
查看习题详情和答案>>
如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且∠DCB=∠EBC=
| 1 | 2 |
小新同学是这样思考的：
在平时的学习中，有这样的经验：假如△ABC是等腰三角形，那么在给定一组对应条件，如图a，BE，CD分别是两底角的平分线（或者如图b，BE，CD分别是两条腰的高线，或者如图c，BE，CD分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角．这个问题也许可以通过添加辅助线构造轴对称图形来解决．请参考小新同学的思路，解决上面这个问题．
解决下面问题：
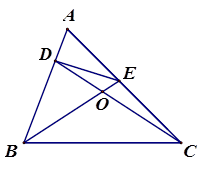
如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且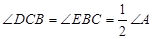
，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．
小新同学是这样思考的：
在平时的学习中，有这样的经验：假如△ABC是等腰三角形，那么在给定一组对应条件，如图a，BE，CD分别是两底角的平分线（或者如图b，BE，CD分别是两条腰的高线，或者如图c，BE，CD分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决．
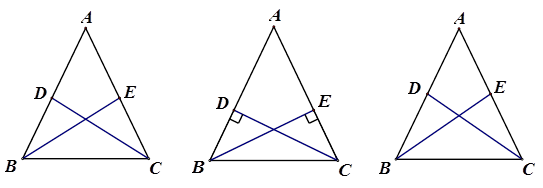
图a 图b 图c
请参考小新同学的思路，解决上面这个问题．.
如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且
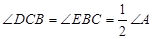，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．小新同学是这样思考的：
在平时的学习中，有这样的经验：假如△ABC是等腰三角形，那么在给定一组对应条件，如图a，BE，CD分别是两底角的平分线（或者如图b，BE，CD分别是两条腰的高线，或者如图c，BE，CD分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决．
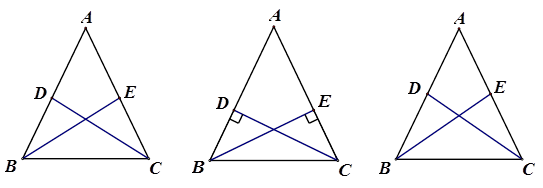
图a 图b 图c
请参考小新同学的思路，解决上面这个问题．.