摘要:⑵依题意.得
网址:http://m.1010jiajiao.com/timu_id_474608[举报]
问题情境:数学活动课上,老师提出了一个问题:如图①,已知在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一动点(点D不与点A,B重合)连接CD,以点C为旋转中心,将CD逆时针旋转90°得到CE,连接BE,试探索线段AB,BD,BE之间的数量关系.
小组展示:“希望”小组展示如下:解:线段AB,BD,BE之间的数量关系是AB=BE+BD.
证明:如图①∵∠ACB=90°,∠DCE=90°
∴∠ACB=∠DCE
∴∠ACB=∠DCB=∠DCE-∠DCB
即∠ACD=∠BCE
∵CE是由CD旋转得到.
∴CE=CD
则在△ACD和△BCE中,
∴△ACD≌△BCE(依据1)
∴AD=BE(依据2)
∵AB=AD+BD
∴AB=BE+BD
反思与交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)“腾飞”小组提出了与“希望”小组不同的意见,认为还有两种情况需要考虑,你根据他们的分类情况直接写出发现的结论:
①如图②,当点D在线段AB的延长线上时,三条点段AB,BD,BE之间的数量关系是 .
②如图③,当点D在线段BA的延长线上时,三条线段AB,BD,BE之间的数量关系是 .
(3)如图④,当点D在线段BA的延长线上时,若CD=4,线段DE的中点为F,连接FB,求FB的长度.

查看习题详情和答案>>
小组展示:“希望”小组展示如下:解:线段AB,BD,BE之间的数量关系是AB=BE+BD.
证明:如图①∵∠ACB=90°,∠DCE=90°
∴∠ACB=∠DCE
∴∠ACB=∠DCB=∠DCE-∠DCB
即∠ACD=∠BCE
∵CE是由CD旋转得到.
∴CE=CD
则在△ACD和△BCE中,
|
∴△ACD≌△BCE(依据1)
∴AD=BE(依据2)
∵AB=AD+BD
∴AB=BE+BD
反思与交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)“腾飞”小组提出了与“希望”小组不同的意见,认为还有两种情况需要考虑,你根据他们的分类情况直接写出发现的结论:
①如图②,当点D在线段AB的延长线上时,三条点段AB,BD,BE之间的数量关系是
②如图③,当点D在线段BA的延长线上时,三条线段AB,BD,BE之间的数量关系是
(3)如图④,当点D在线段BA的延长线上时,若CD=4,线段DE的中点为F,连接FB,求FB的长度.

注意:为了使同学们更好地解答本题,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
某书店去图书交易市场购买某种图书,第一次用1200元购买若干本,第二次购书时每本的进价是上一次的1.2倍,用1500元购得图书数量比第一次多10本.
(1)求第一次购买图书的进价是多少元?
(2)该书店第一次购进的图书按书上标价7元出售的,很快售完;第二次购进的图书当按书上的标价7元售出200本后,出现滞销,便以书上标价的4折售完剩余图书,问该书店两次售书总共获利多少元?
解题思路:设第一次购书时每本的进价是x元
(1)①用含x的式子表示:
第一次用1200元购买图书______本;第二次用1500元购得图书______本.
②列出方程,并完成本题第一问的解答.
(2)用数填空:
①第一次购进图书______本,第一次获利______元.
②列出式子,并完成本题第二问的解答.
查看习题详情和答案>>
某书店去图书交易市场购买某种图书,第一次用1200元购买若干本,第二次购书时每本的进价是上一次的1.2倍,用1500元购得图书数量比第一次多10本.
(1)求第一次购买图书的进价是多少元?
(2)该书店第一次购进的图书按书上标价7元出售的,很快售完;第二次购进的图书当按书上的标价7元售出200本后,出现滞销,便以书上标价的4折售完剩余图书,问该书店两次售书总共获利多少元?
解题思路:设第一次购书时每本的进价是x元
(1)①用含x的式子表示:
第一次用1200元购买图书______本;第二次用1500元购得图书______本.
②列出方程,并完成本题第一问的解答.
(2)用数填空:
①第一次购进图书______本,第一次获利______元.
②列出式子,并完成本题第二问的解答.
查看习题详情和答案>>
阅读题:我国著名数学家华罗庚说过:“数缺形时少直观,形小数时难入微,数形结合百般好,隔离分家事万休.”数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例:求1+2+3+4+…+n的值,其中n是正整数;
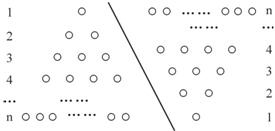
如果采用数形结合的方法,现利用图形的性质来求1+2+3+4+…+n的值,方案如下:
如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3…n个小圆圈的个数恰好为所求式子1+2+3+4+…+n的值,为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为
,即1+2+3+4+…+n=
①仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中n为正整数(要求画出图形,写出结果即可)
②试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数(要求画出图形,写出结果即可)
 查看习题详情和答案>>
查看习题详情和答案>>
例:求1+2+3+4+…+n的值,其中n是正整数;
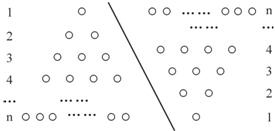
如果采用数形结合的方法,现利用图形的性质来求1+2+3+4+…+n的值,方案如下:
如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3…n个小圆圈的个数恰好为所求式子1+2+3+4+…+n的值,为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
①仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中n为正整数(要求画出图形,写出结果即可)
②试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数(要求画出图形,写出结果即可)
 查看习题详情和答案>>
查看习题详情和答案>>
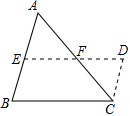 如图,任意△ABC中,可沿中位线EF一刀剪切后,用得到的△AEF和四边形EBCF可拼成?EBCD,现在仿上述方法,结合自己所画的图,完成下列问题.
如图,任意△ABC中,可沿中位线EF一刀剪切后,用得到的△AEF和四边形EBCF可拼成?EBCD,现在仿上述方法,结合自己所画的图,完成下列问题.(1)在△ABC中,可增加条件
(2)在△ABC中,可增加条件
(3)在△ABC中,可增加条件
(要求依照例图,在指定的位置画好对应的图形,不用证明) 查看习题详情和答案>>
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=