题目内容
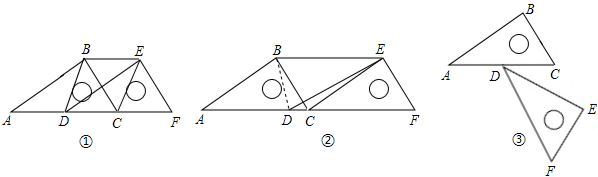
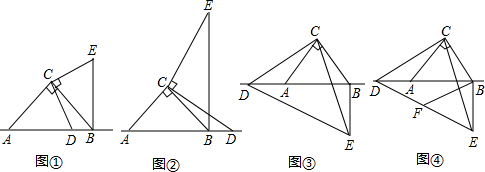
问题情境:数学活动课上,老师提出了一个问题:如图①,已知在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一动点(点D不与点A,B重合)连接CD,以点C为旋转中心,将CD逆时针旋转90°得到CE,连接BE,试探索线段AB,BD,BE之间的数量关系.
小组展示:“希望”小组展示如下:解:线段AB,BD,BE之间的数量关系是AB=BE+BD.
证明:如图①∵∠ACB=90°,∠DCE=90°
∴∠ACB=∠DCE
∴∠ACB=∠DCB=∠DCE-∠DCB
即∠ACD=∠BCE
∵CE是由CD旋转得到.
∴CE=CD
则在△ACD和△BCE中,
∴△ACD≌△BCE(依据1)
∴AD=BE(依据2)
∵AB=AD+BD
∴AB=BE+BD
反思与交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)“腾飞”小组提出了与“希望”小组不同的意见,认为还有两种情况需要考虑,你根据他们的分类情况直接写出发现的结论:
①如图②,当点D在线段AB的延长线上时,三条点段AB,BD,BE之间的数量关系是 .
②如图③,当点D在线段BA的延长线上时,三条线段AB,BD,BE之间的数量关系是 .
(3)如图④,当点D在线段BA的延长线上时,若CD=4,线段DE的中点为F,连接FB,求FB的长度.
小组展示:“希望”小组展示如下:解:线段AB,BD,BE之间的数量关系是AB=BE+BD.
证明:如图①∵∠ACB=90°,∠DCE=90°
∴∠ACB=∠DCE
∴∠ACB=∠DCB=∠DCE-∠DCB
即∠ACD=∠BCE
∵CE是由CD旋转得到.
∴CE=CD
则在△ACD和△BCE中,
|
∴△ACD≌△BCE(依据1)
∴AD=BE(依据2)
∵AB=AD+BD
∴AB=BE+BD
反思与交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)“腾飞”小组提出了与“希望”小组不同的意见,认为还有两种情况需要考虑,你根据他们的分类情况直接写出发现的结论:
①如图②,当点D在线段AB的延长线上时,三条点段AB,BD,BE之间的数量关系是
②如图③,当点D在线段BA的延长线上时,三条线段AB,BD,BE之间的数量关系是
(3)如图④,当点D在线段BA的延长线上时,若CD=4,线段DE的中点为F,连接FB,求FB的长度.

练习册系列答案
相关题目
下列说法中,错误的是( )
| A、一组对边平行且相等的四边形是平行四边形 | B、两条对角线互相垂直且平分的四边形是菱形 | C、四个角都相等的四边形是矩形 | D、邻边都相等的四边形是正方形 |
若正多边形的一个内角等于144°,则这个正多边形的边数是( )
| A、9 | B、10 | C、11 | D、12 |
已知∠A=40°18′,∠B=40°17′30″,∠C=40.18°,则( )
| A、∠A>∠B>∠C | B、∠B>∠A>∠C | C、∠C>∠A>∠B | D、∠A>∠C>∠B |
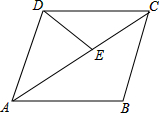 如图,已知四边形ABCD是菱形,过顶点D作DE⊥AD,交对角线AC于点E,若∠DAE=20°,则∠CDE的度数是( )
如图,已知四边形ABCD是菱形,过顶点D作DE⊥AD,交对角线AC于点E,若∠DAE=20°,则∠CDE的度数是( )| A、70° | B、60° | C、50° | D、40° |


 如图,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
如图,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].