摘要:法二:故.可得.
网址:http://m.1010jiajiao.com/timu_id_474555[举报]
(1)作图题:(不要求写作法)
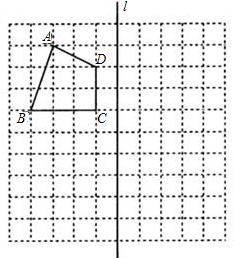
如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上).
①在给出的方格纸中,画出四边形ABCD向下平移5格后的四边形A1B1C1D1;
②在给出的方格纸中,画出四边形ABCD关于直线l对称的图形A2B2C2D2.
(2)某班举行演讲革命故事的比赛中有一个抽奖活动.活动规则是:进入最后决赛的甲、乙两位同学,每人只有一次抽奖机会,在如图所示的翻奖牌正面的4个数字中任选一个数字,选中后可以得到该数字后面的奖品,第一人选中的数字,第二人就不能再选择该数字.
①求第一位抽奖的同学抽中文具与计算器的概率分别是多少?
②有同学认为,如果甲先抽,那么他抽到海宝的概率会大些,你同意这种说法吗?说明理由.
翻奖牌正面:
翻奖牌背面:
查看习题详情和答案>>
如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上).
①在给出的方格纸中,画出四边形ABCD向下平移5格后的四边形A1B1C1D1;
②在给出的方格纸中,画出四边形ABCD关于直线l对称的图形A2B2C2D2.

(2)某班举行演讲革命故事的比赛中有一个抽奖活动.活动规则是:进入最后决赛的甲、乙两位同学,每人只有一次抽奖机会,在如图所示的翻奖牌正面的4个数字中任选一个数字,选中后可以得到该数字后面的奖品,第一人选中的数字,第二人就不能再选择该数字.
①求第一位抽奖的同学抽中文具与计算器的概率分别是多少?
②有同学认为,如果甲先抽,那么他抽到海宝的概率会大些,你同意这种说法吗?说明理由.
翻奖牌正面:
| 1 | 2 |
| 3 | 4 |
| 文具 | 计算器 |
| 计算器 | 海宝 |
(1)作图题:(不要求写作法)
如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上).
①在给出的方格纸中,画出四边形ABCD向下平移5格后的四边形A1B1C1D1;
②在给出的方格纸中,画出四边形ABCD关于直线l对称的图形A2B2C2D2.

(2)某班举行演讲革命故事的比赛中有一个抽奖活动.活动规则是:进入最后决赛的甲、乙两位同学,每人只有一次抽奖机会,在如图所示的翻奖牌正面的4个数字中任选一个数字,选中后可以得到该数字后面的奖品,第一人选中的数字,第二人就不能再选择该数字.
①求第一位抽奖的同学抽中文具与计算器的概率分别是多少?
②有同学认为,如果甲先抽,那么他抽到海宝的概率会大些,你同意这种说法吗?说明理由.
翻奖牌正面:
| 1 | 2 |
| 3 | 4 |
| 文具 | 计算器 |
| 计算器 | 海宝 |
同学们应该听说过“苏武牧羊”的故事吧,这个被传诵了一千多年的故事可用这样一首诗来表述:当年苏武去北边,不知去了几多年,分明记得天边月,二百三十五番圆.同学们都能读懂苏武去北方一共牧了二百三十五个月的羊,那么他牧羊的时间应为________年.(注:古代有“十九年七闰”的说法)
查看习题详情和答案>>先阅读,再利用其结论解决问题.
阅读:已知一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1,x2,则有x1+x2=﹣,x1•x2=.这个结论是法国数学家韦达最先发现并证明的,故把它称为“韦达定理”.利用此定理,可以不解方程就得出x1+x2和 x1•x2的值,进而求出相关的代数式的值.
解决问题:对于一切不小于2的自然数n,关于x的一元二次方程x2﹣(n+2)x﹣2n2=0的两个根记作an,bn(n≥2),
请求出
![]()
![]() +…
+…![]() 的值.
的值.
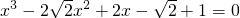 ,这是一个高次方程,我们未学过其解法,难以求解.如果我们换一个角度(“已知”和“未知”互换),即将
,这是一个高次方程,我们未学过其解法,难以求解.如果我们换一个角度(“已知”和“未知”互换),即将 看做“未知数”,而将x看成“已知数”,则原方程可整理成:
看做“未知数”,而将x看成“已知数”,则原方程可整理成: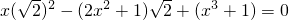 .
.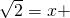 1或
1或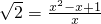 .
.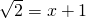 和一个一元二次方程x2-x+1=
和一个一元二次方程x2-x+1= ,从而不难求得这个高次方程的解.
,从而不难求得这个高次方程的解.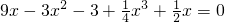 .
.