摘要:因为平面.
网址:http://m.1010jiajiao.com/timu_id_474042[举报]
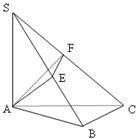
如图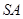 ⊥平面
⊥平面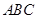 ,
,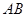 ⊥
⊥ ,过
,过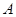 做
做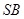
的垂线,垂足为 ,过
,过 做
做 的垂线,垂足为
的垂线,垂足为
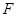 ,求证
,求证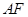 ⊥
⊥ 。以下是证明过程:
。以下是证明过程:
要证
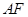 ⊥
⊥
只需证  ⊥平面
⊥平面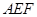
只需证 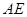 ⊥
⊥ (因为
(因为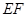 ⊥
⊥ )
)
只需证 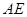 ⊥平面
⊥平面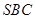
只需证 ① (因为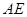 ⊥
⊥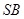 )
)
只需证  ⊥平面
⊥平面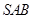
只需证 ② (因为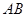 ⊥
⊥ )
)
由只需证 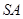 ⊥平面
⊥平面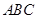 可知上式成立
可知上式成立
所以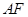 ⊥
⊥
把证明过程补充完整① ②
查看习题详情和答案>>
在平面直角坐标系 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值.
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)曲线 与
与 轴的交点为(0,1),
轴的交点为(0,1),
与 轴的交点为(3+2
轴的交点为(3+2 ,0),(3-2
,0),(3-2 ,0) 故可设
,0) 故可设 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因为圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 。联立方程组得到结论。
。联立方程组得到结论。
查看习题详情和答案>>
 中,曲线
中,曲线 的参数方程为
的参数方程为 点
点 是曲线
是曲线 的中点
的中点 的轨迹的直角坐标方程;
的轨迹的直角坐标方程; 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,若直线
轴的正半轴为极轴建立极坐标系,若直线 的极坐标方程为
的极坐标方程为 ,求点
,求点 ,由中点坐标公式可得
,由中点坐标公式可得 所以点
所以点 消参可得
消参可得
 ,因为原点到直线的距离为
,因为原点到直线的距离为 ,
,
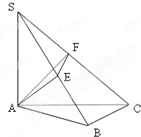 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程: